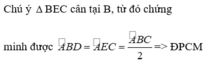1.cho tam giác ABC.tia phân giác góc B cắt AC ở D.trên tia BA lấy điểm Esao cho BÉ=BC.CM :BD vuông góc vs EC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2016
BD là phân giác ABC nên ABD = CBD
Có: ABD + CBD + BEC = 180o
=> 2.CBD + BEC = 180o (1)
Tam giác BEC có: BE = BC (gt) nên tam giác BEC cân tại B
=> BEC = BCE ( tính chất tam giác cân)
Tam giác BEC có: BEC + BCE + CEB = 180o ( tổng 3 góc của tam giác)
=> 2.BCE + CEB = 180o (2)
Từ (1) và (2) => CBD = BCE
Mà CBD và BCE là 2 góc ở vị trí so le trong nên BD // EC (đpcm)
M
30 tháng 7 2017
Xét tam giác BCE có BC=BE => tam giác BCE cân tại B.
do đó góc C=E. ( T/C tam giác cân )
ta có : B1+B2+B3=180o
C+E+B =180o
Mà góc C=E ; B1=B2 (VÌ BD là phân giác của góc B)
=> GÓC 2C=180=2B2
=> 2C=2B2
=> C=B2
Mà chúng ở vị chí so le trong
=> BD // CE (đpcm)
16 tháng 12 2022
a:Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
=>DB=DE
b: ΔABD=ΔAED
nên góc BDA=góc EDA
=>DA là phân giác của góc BDE
c: Xét ΔDBI và ΔDEC có
BI=EC
góc DBI=góc DEC
DB=DE
Do đó: ΔDBI=DEC
=>góc BDI=góc EDC
=>góc BDI+góc BDE=180 độ
=>I,D,E thẳng hàng
16 tháng 12 2021
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
