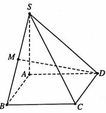
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a có S A ⊥ A B C D và SA = a 2 . Gọi M là trung điểm SB (tham khảo hình vẽ bên). Tính tan của góc giữa đường thẳng DM và (ABCD).
A. 5 5
B. 2 5
C. 2 5
D. 10 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi H là trung điểm AB Khi đó, MH ∥ SA nên M H ⊥ ( A B C D ) góc giữa DM và (ABCD) là góc M D H ^
Ta có M H = S A 2 = a 2 2 ; D H = A H 2 + A D 2 = a 5 2
Xét tam giác MDH vuông tại H có tan M D H ^ = M H D H = 10 5

Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .