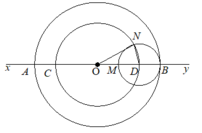
Trên đường thẳng xy lấy một điểm O. Vẽ đường tròn (O;3cm) cắt Ox, Oy theo thứ tự tại A, B. Vẽ đường tròn (O;2cm) cắt Ox, Oy theo thứ tự tại C, D. Vẽ đường tròn (D;DB) cắt BO tại M và cắt đường tròn (O;2cm) tại N. So sánh AC, BD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
30 tháng 9 2021
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
Suy ra: \(\widehat{MAB}=\widehat{MBA}\)
Xét ΔDAB vuông tại D và ΔEBA vuông tại E có
BA chung
\(\widehat{DBA}=\widehat{EAB}\)
Do đó: ΔDAB=ΔEBA
Suy ra: \(\widehat{DAB}=\widehat{EBA}\)
hay \(\widehat{HAB}=\widehat{HBA}\)
Xét ΔHBA có \(\widehat{HAB}=\widehat{HBA}\)
nên ΔHBA cân tại H
Suy ra: HA=HB
hay H nằm trên đường trung trực của AB(1)
Ta có:MA=MB
nên M nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,M thẳng hàng
CM
25 tháng 12 2018
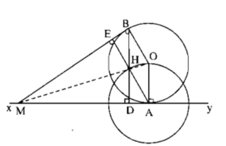
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
