Cho điểm O thuộc đường thẳng xy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Hỏi trong ba điểm O, A, B, điểm nào nằm giữa hai điểm còn lại? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đăng Nhân
CTVHS
4 tháng 4 2023
Từ bài toán, ta có hình ảnh:
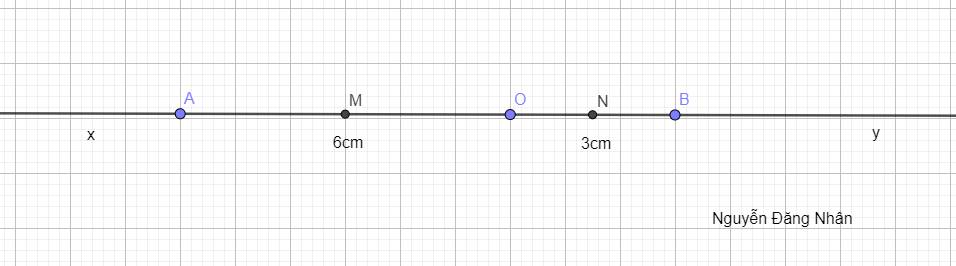
A) Vì M nằm ở tia Ox (bên trái O), N nằm ở tia Oy (bên phải O) nên điểm nằm giữa 2 điểm còn lại là điểm O (nằm giữa M và N)
B) Vì M là trung điểm OA, ta có:
\(OM=\dfrac{OA}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Tương tự, N là trung điểm của OB, ta có:
\(ON=\dfrac{OB}{2}=\dfrac{3}{2}=1,5\left(cm\right)\)
Vì O nằm giữa MN (ở phần A), nên ta có:
\(MN=OM+ON=3+1,5=4,5\left(cm\right)\)
12 tháng 4 2022
a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
b: Trên tia Ox, ta có: OA<OC
nên điểm A nằm giữa hai điểm O và C
=>OA+AC=OC
hay AC=3(cm)
Ta có: A nằm giữa O và C
mà AO=AC
nên A là trung điểm của OC
16 tháng 3 2023
a. Để xác định điểm nào nằm giữa hai điểm còn lại, ta cần so sánh độ dài các cạnh. Ta có:
OA = 3 cm < OC = 6 cm, nên A nằm giữa O và C.
OB = 8 cm > OC = 6 cm, nên B không nằm giữa O và C. Vậy điểm A nằm giữa B và C.
b. Để xác định xem điểm A có phải trung tâm của đoạn thẳng OC hay không, ta cần tính độ dài các cạnh. Ta có: OA = 3 cm, OC = 6 cm. Nếu A là trung tâm của OC, thì ta có: OA = AC = OC/2 = 6/2 = 3 cm. Vậy ta thấy A không phải trung tâm của OC vì OA ≠ AC.
c. Để so sánh độ dài đoạn thẳng AD và OB, ta cần tính độ dài các cạnh. Ta có: OD = 6 cm, OA = 3 cm, OB = 8 cm. Áp dụng định lí Pytago:
Tam giác OAD vuông tại A, có cạnh huyền là OD, nên: AD² = OA² + OD² = 3² + 6² = 45 cm²
Tam giác OAB vuông tại A, có cạnh huyền là OB, nên: AB² = OA² + OB² = 3² + 8² = 73 cm². Do đó, ta có: AD² < AB² => AD < AB. Vậy độ dài đoạn thẳng AD nhỏ hơn độ dài đoạn thẳng OB.
15 tháng 10 2015
giải cụ thể ra giúp mình đi! Năn nỉ bạn đó! Vẽ hình luôn!
5 tháng 8 2017
a)2 tia đối nhau gốc O là Ox,Oy
b) vì O nằm trên đường thẳng xy
mà điểm M thuộc tia Oy
điểm N thuộc tia Ox
=>O nằm giữa M,N
Điểm O nằm giữa hai điểm A và B.