Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
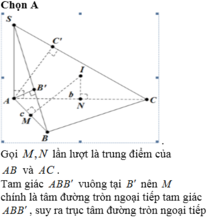
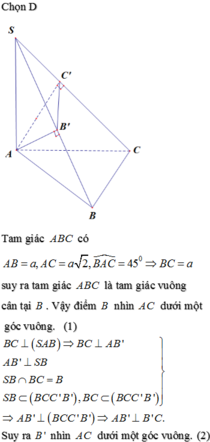
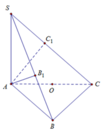
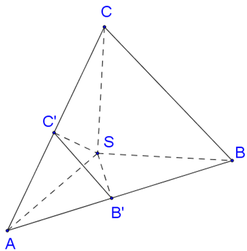
, AC = b, AB = c, ![]() . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c,
α
.
. Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c,
α
.
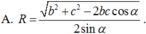
![]()
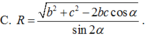
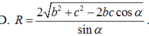

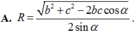
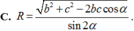
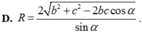

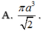





Đáp án đúng : A