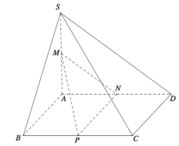
Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, B A C ^ = 120 ° . Cạnh bên S A = 2 3 vuông góc với mặt phẳng đáy (ABCD). Gọi M,N,P lần lượt là trung điểm các cạnh SA, ADvà BC, α là góc giữa hai mặt phẳng (SAC) và (MNP). Chọn khẳng định đúng trong các khẳng định sau đây
![]()
![]()
![]()
![]()

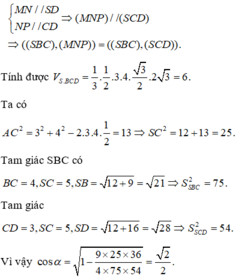

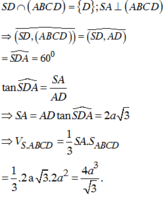
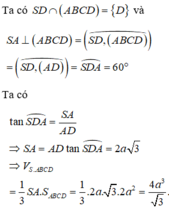
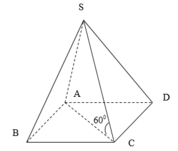
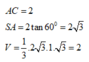
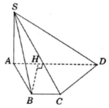
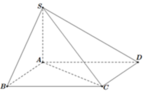
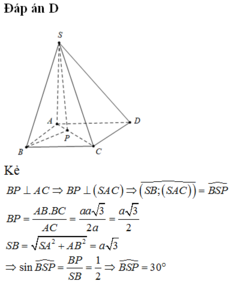
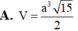
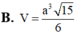
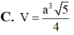
Đáp án A.