Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC = 1 . Trên hai tia Ox,Oy lần lượt lấy hai điểm A,B thay đổi sao cho OA + OB = OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC ?
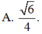
![]()
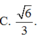
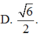
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử
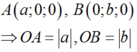
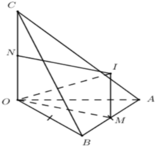
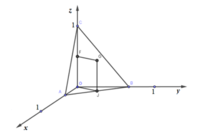
Tứ diện OABC có OA, OB, OC đôi một vuông góc.
Gọi M, N lần lượt là trung điểm của AB và OC.
Ta có
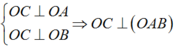
Qua M dựng đường thẳng song song với OC, qua N dựng đường thẳng song song với OM. Hai đường thẳng này cắt nhau tại I.
∆ O A B vuông tại O ⇒ M là tâm đường tròn ngoại tiếp ∆ O A B ⇒ I A = I B = I O .
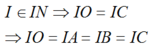
I là tâm mặt cầu ngoại tiếp O.ABC
Ta có
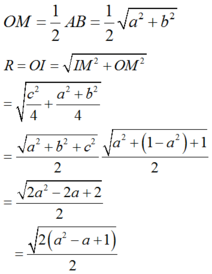
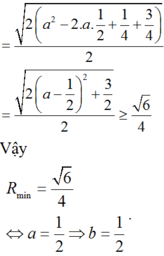
Chọn A.

Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y > 0)
Vì OA + OB = OC = 1 => x + y = 1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
∆OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác.
GJ // OC => GJ ⊥ (OAB) => GO = GA = GB
GF // JO, JO ⊥ OC => GF ⊥ OC, mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC = GO
=> GO = GA = GB = GC => G là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC :
![]()
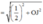
Ta có:
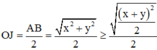
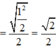
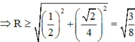
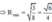

Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y>0)
Vì OA+OB=OC = 1 => x+y=1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G
Tam giác OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác
![]()
![]()
mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC=GO
=> GO=GA=GB=GC=> G là tâm mặt cầu ngoại tiếp tứ diện OABC.
Bán kính mặt cầu ngoại tiếp tứ diện OABC
![]()
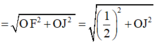
Ta có:
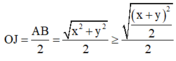
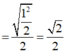
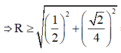
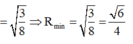

HD: Gọi tọa độ ba điểm A, B, C lần lượt là

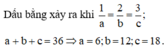
Vậy độ dài ba cạnh OA, OB, OC lần lượt theo thứ tự lập thành cấp số cộng. Chọn C.

Đáp án A
Dễ dàng suy ra:
A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , a , b , c > 0
vì d M ; O B C = d M ; O y z = x M = 1 , tương tự ta có được M 1 ; 2 ; 3
M ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 1.2.3 a . b . c 3 ⇔ a b c 6 = V O . A B C ≥ 27
Dấu bằng xảy ra khi:
1 a = 2 b = 3 c = 1 3 ⇒ a = 3 ; b = 6 ; c = 9 ⇒ a + b + c = 18
Đáp án đúng : A