Cho hai mặt cầu ( S 1 ) có tâm I 1 , bán kính R 1 = 1 , ( S 2 ) có tâm I 2 bán kính R 2 = 5. Lần lượt lấy hai điểm M 1 , M 2 thuộc hai mặt cầu ( S 1 ) , ( S 2 ) . Gọi K là trung điểm M 1 M 2 . Khi M 1 M 2 di chuyển trên ( S 1 ) , ( S 2 ) thì K quét miền không gian là một khối tròn xoay có thể tích bằng?
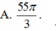
![]()
![]()

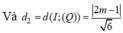
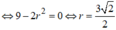
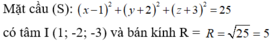
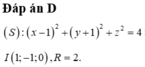

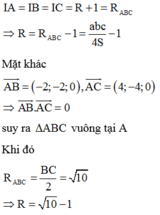



Đáp án đúng : C