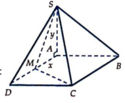
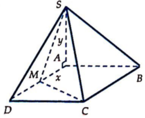
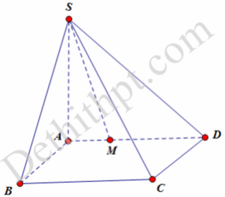
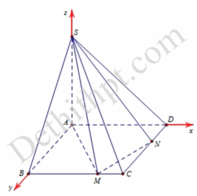
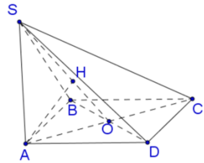
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = y > 0 và vuông góc với đáy. Trên AD lấy điểm M, đặt AM = x (0 < x < a) . Nếu x 2 + y 2 = a 2 thì giá trị lớn nhất của thể tích S.ABCM bằng:
A. a 3 3 3
B. a 3 3 8
C. a 3 3 24
D. 3 a 3 3 8

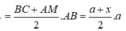
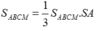
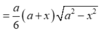
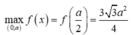
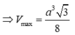
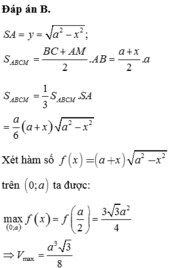

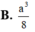
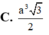
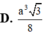
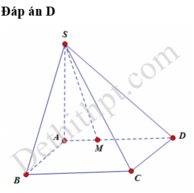
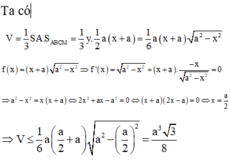



Đáp án B
S A = y = a 2 - x 2 ; S A B C M = B C + A M 2 . A B = a + x 2 . a
S A B C M = 1 3 S A B C M . S A = a 6 ( a + x ) a 2 - x 2
Xét hàm số f ( x ) = ( a + x ) a 2 - x 2 trên 0 ; a ta được:
m a x 0 ; a f ( x ) = f a 2 = 3 3 a 2 4 ⇒ V m a x = a 3 3 8