Trong không gian Oxyz cho mặt cầu ( S ) : x - 1 2 + y + 2 2 + z - 3 2 = 27 . Gọi α là mặt phẳng đi qua hai điểm A(0;0;-4) và B(2;0;0) cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng α có phương trình dạng ax+by-z+c=0, khi đó a-b+c bằng:
A. -4.
B. 8.
C. 0.
D. 2.


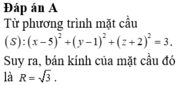
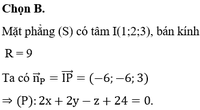

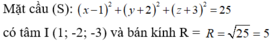


Đáp án C
( S ) : x - 1 2 + y + 2 2 + z - 3 2 = 27
=> I(1;-2;3), R= 3 3
A(0;0;-4) và B(2;0;0) α : ax+by-z+c=0
Ta có:
Ta có: V = 1 3 π 27 - r 2 . r 2