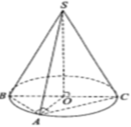
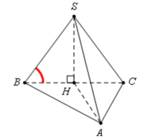
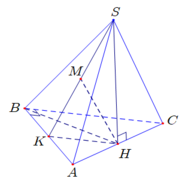
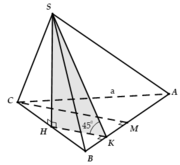
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng A B = a , A C = a 3 đường thẳng SA tạo với đáy một góc 60 ∘ .Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi l là độ dài đường sinh hình nón. Tính l.
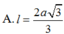
![]()
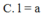
![]()

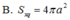
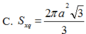


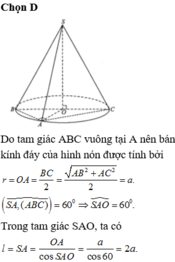
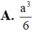
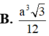
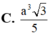
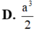
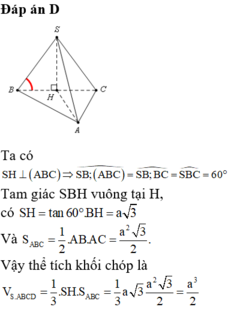



Đáp án đúng : D