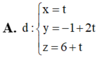
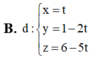
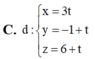
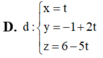
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án D
Mặt phẳng (P) có vec-tơ pháp tuyến là n P ⇀ = 1 ; m ; - 1
Mặt phẳng (Q) có vec-tơ pháp tuyến là n Q ⇀ = m ; - 1 ; 1
Đường thẳng d m là giao tuyến của hai mặt phẳng (P) và (Q) nên có một vec- tơ chỉ phương là
Mặt phẳng (P) có vec-tơ pháp tuyến là n R ⇀ = 3 ; 1 ; 2
Để d m ⊥ R ⇔ Hai vec-tơ u ⇀ và n R ⇀ cùng phương
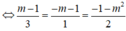
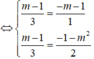
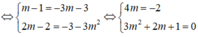
⇒ Không tồn tại giá trị m thỏa mãn yêu cầu bài toán.
Đáp án C
Gọi A Î D Þ Tọa độ của A thỏa mãn hệ PT
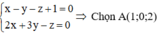
Phương trình chính tắc của đường thẳng giao tuyến D là
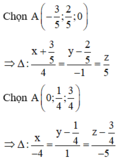
Đáp án D
Ta có:
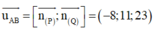
Do đó A B → phương với véc tơ u → = ( 8 ; - 11 ; - 23 )
Đáp án D
Phương pháp giải:
Ứng dụng tích có hướng để tìm vectơ chỉ phương của đường thẳng giao tuyến và giải hệ phương trình để tìm tọa độ giao điểm của hai mặt phẳng
Lời giải: Ta có
Gọi d là giao tuyến của (P) và (Q).
Ta có
Xét hệ
Vậy phương trình đường thẳng cần tìm là