Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]. Khi đó số phần tử của S là
A. 11
B. 10
C. Vô số
D. 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1

Chọn D
Xét hàm số y =
x
2
-
m
x
+
2
m
x
-
2
trên [-1;1] có: 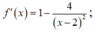
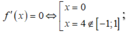
![]()
Bảng biến thiên

Trường hợp 1. ![]() Khi đó
Khi đó
![]()
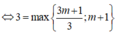
![]()
Trường hợp 2. ![]()
Khả năng 1. 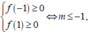
Khi đó ![]()
Khả năng 2 ![]() Khi đó
Khi đó 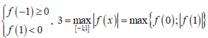
![]() Trường hợp này vô nghiệm.
Trường hợp này vô nghiệm.
Khả năng 3. ![]() Khi đó
Khi đó ![]() Vô nghiệm.
Vô nghiệm.
Vậy có hai giá trị thỏa mãn là ![]() Do đó tổng tất cả các phần tử của S là -1.
Do đó tổng tất cả các phần tử của S là -1.
Chọn A
Đặt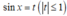 ta có:
ta có: 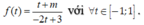
Ta có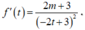
Do m ∈ Z nên ta xét hai trường hợp sau
+TH1: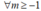 thì hàm số đồng biến trên [-1;1].
thì hàm số đồng biến trên [-1;1].
Xét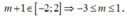
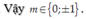
+TH2: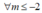 thì hàm số nghịch biến trên [-1;1]
thì hàm số nghịch biến trên [-1;1]
Xét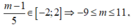
Vậy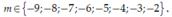
Vậy tập S có 4 phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]