Trong không gian Oxyz, cho đường thẳng d : x - 2 1 = y - 1 - 2 = z - 1 2 và hai điểm A(3;2;1), B(2;0;4). Gọi là ∆ đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến ∆ là nhỏ nhất. Gọi u → =(2;b;c) là một VTCP của ∆ . Khi đó, u → bằng
A. 17
B. 5
C. 6
D. 3

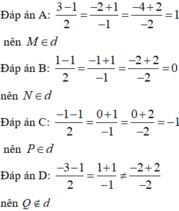
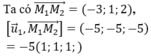
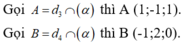
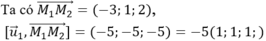

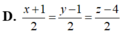
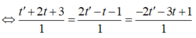
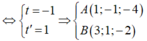


Đáp án B
Cách giải:
d : x - 2 1 = y - 1 - 2 = z - 1 2 có 1 VTCP v → =(1;-2;2) là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d ⇒ ∆ ⊂ ( α ) mặt phẳng qua A và vuông góc d mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng α
khi và chỉ khi đi qua hình chiếu H của B lên α
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của α có phương trình: