Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2
A. -4
B. -2
C. -1
D. -3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Hàm số y = f(x) = 2 x + m x - 1 . xác định và liên tục trên [2;3].
Với m = -2, hàm số trở thành y = 2![]() (không thỏa)
(không thỏa)
Với ![]() ta có:
ta có: 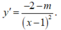
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra 
Do đó: ![]()
![]()
Theo giả thiết ![]()
![]()
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức ![]() là không cần thiết.
là không cần thiết.

- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)

Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)

Với \(m=-2\) ko thỏa mãn
Với \(m\ne-2\) hàm \(f\left(x\right)\) là bậc nhất trên bậc nhất nên luôn đơn điệu trên khoảng đã cho
\(\Rightarrow\) min max rơi vào 2 đầu mút
\(f\left(2\right)=m+4\) ; \(f\left(3\right)=\dfrac{m+6}{2}\)
\(\Rightarrow\left|m+4-\dfrac{m+6}{2}\right|=2\Leftrightarrow\)
\(\Leftrightarrow m+2=\pm4\Rightarrow\left[{}\begin{matrix}m=2\\m=-6\end{matrix}\right.\)

\(h\left(x\right)=x^2-4x+5+m\)
\(g\left(x\right)=\left|h\left(x\right)\right|=\left|f\left(x\right)+m\right|=\left|x^2-4x+5+m\right|\)
\(h\left(0\right)=5+m;h\left(4\right)=5+m;h\left(2\right)=1+m\)
TH1: \(1+m>0\Leftrightarrow m>-1\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
TH2: \(5+m< 0\Leftrightarrow m< -5\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
TH3: \(5+m>0>1+m\Leftrightarrow-5< m< -1\)
Nếu \(5+m< -1-m\Leftrightarrow m< -3\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
Nếu \(5+m=-1-m\Leftrightarrow m=-3\)
\(max=5+m=2\ne9\)
\(\Rightarrow m=-3\) không thỏa mãn yêu cầu bài toán
Nếu \(5+m>-1-m\Leftrightarrow m>-3\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
Vậy \(m=4;m=-10\)
Chọn A
Hàm số y = f(x) = 2 x + m x - 1 xác định và liên tục trên [2;3]
Với m = -2, hàm số trở thành y = 2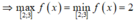 (không thỏa).
(không thỏa).
Với m ≠ 2, ta có: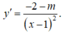
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra
Do đó:
Theo giả thiết
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức là không cần thiết.
là không cần thiết.