Cho hàm số y = x - 3 x + 1 có đồ thị (C) và một điểm A ∈ C . Tiếp tuyến với đồ thị tại A tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất bằng bao nhiêu
A. 2 + 2 2
B. 4 - 2 2
C. 3 - 2
D. 4 + 2 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 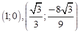 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
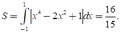
Chọn D.
Chọn đáp án B
Đạo hàm
Đường thẳng ∆ là tiếp tuyến của đồ thị (C) tại ∆ nên có hệ số góc là
Phương trình ∆
Đồ thị (C) có đường tiệm cận đứng là ∆ 1 : x = - 1 và đường tiệm cận ngang là ∆ 2 : y = 1
Nửa chu vi tam giác IMN là
Dấu "=" xảy ra khi
Bán kính đường tròn nội tiếp tam giác IMN là