Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
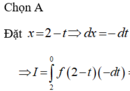
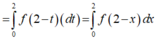
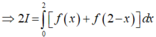
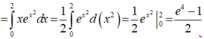
Xét tích phân J = ∫ - π 2 π 2 f - x d x
Đặt: x = -t nên dx = -dt
Đổi cận
x = = - π 2 ⇒ t = π 2 x = π 2 ⇒ t = - π 2
Khi đó
I = ∫ - π 2 π 2 f - t d t = J ⇒ 3 I + 2 I = ∫ - π 2 π 2 f - x + 2 f x d x = ∫ - π 2 π 2 cos x d x = 2
Vậy I = 2 3
Đáp án B
Đáp án C
Cách 1: Thay x bởi -x ta được f x + 2 f − x = cos − x = cos x . Kết hợp với giả thiết ta có
f − x + 2 f x = f x + 2 f − x ⇔ f x = f − x
Suy ra f x = 1 3 cos x . Vậy I = ∫ − π 2 π 2 f x d x = 1 3 ∫ − π 2 π 2 cos x d x = 2 3 .
Cách 2: Từ giả thiết ta có ∫ − π 2 π 2 f − x + 2 f x d x = ∫ − π 2 π 2 cos x d x
⇔ ∫ − π 2 π 2 f − x d x + 2 ∫ − π 2 π 2 f x d x = 2 ⇔ ∫ − π 2 π 2 f t d t + 2 ∫ − π 2 π 2 f x d x = 2 ⇔ ∫ − π 2 π 2 f x d x = 2 3 .
Xét tích phân I = ∫ - π 2 π 2 f x d x
Đặt x = -t nên dx = -dt
Đổi cận x = - π 2 ⇒ t = π 2 ; x = π 2 ⇒ t = - π 2
Khi đó
I = ∫ - π 2 π 2 f - t d t = J ⇒ 3 I = J + 2 I = ∫ - π 2 π 2 f - x + 2 f x d x = J = ∫ - π 2 π 2 cos x d x = 2
Vậy I = 2 3
Đáp án B
.
.
.
.
