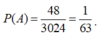Gọi S là tập hợp tất các cả số tự nhiên gồm bốn chữ số. Chọn ngẫu nhiên một số từ S, xác suất để số chọn được có bốn chữ số khác nhau bằng
A. 14 25
B. 63 125
C. 2 25
D. 18 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
Gọi số tự nhiên có bốn chữ số thỏa mãn yêu cầu bài toán là ![]()
Số phần tử của không gian mẫu là ![]()
Gọi biến cố A ‘‘Số được chọn lớn hơn số 6700’’.
Ta các TH sau:
TH1: có 1 cách chọn.
![]() có 3 cách chọn.
có 3 cách chọn.
+ Các chữ số c,d được chọn từ 8 chữ số còn lại có sắp thứ tự và số cách chọn là A 8 2
Số cách để chọn ở trường hợp 1 là: 3. A 8 2
TH2 : ![]() có 3 cách chọn. Khi đó: b,c,d có
A
9
3
cách chọn.
có 3 cách chọn. Khi đó: b,c,d có
A
9
3
cách chọn.
Số cách để chọn ở trường hợp 1 là: 3. A 9 3
Như vậy, ta được n(A) = 3. A 8 2 + 3. A 9 3 = 1680
Suy ra 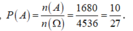

Chọn A
+) Không gian mẫu Ω = “Chọn ngẫu nhiên một số trong các số tự nhiên có 3 chữ số”.=> | Ω | = 9. 10 2
+) Biến cố A = “Số tự nhiên được chọn chia hết cho 9 và các chữ số đôi một khác nhau”.
Ta tìm số các số tự nhiên gồm 3 chữ số khác nhau và chia hết cho 9 (tổng các chữ số là một số chia hết cho 9).
Bộ ba số (a;b;c) với a,b,c ∈ [0;9](a,b,c đôi một khác nhau ) và a + b + c = 9m, m ∈ ℕ * được liệt kê dưới đây:

Vậy có tất cả 10.3! + 4.2.2! = 76 => | Ω A | = 76
Xác suất cần tính bằng 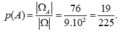

Không gian mẫu: \(A_7^3-A_6^2=180\) số
Các trường hợp số chữ số lẻ nhiều hơn số chữ số chẵn là: 3 chữ số đều lẻ, 2 chữ số lẻ 1 số chữ chẵn
- 3 chữ số đều lẻ: \(A_3^3=3\) số
- 2 chữ số lẻ 1 chữ số chẵn: chọn 2 chữ số lẻ từ 3 chữ số lẻ có \(C_3^2=3\) cách
+ Nếu chữ số chẵn là 0 \(\Rightarrow\) \(3!-2!=4\) cách hoán vị 3 chữ số
+ Nếu chữ số chẵn khác 0 \(\Rightarrow\) có 3 cách chọn chữ số chẵn và \(3!\) cách hoán vị các chữ số
\(\Rightarrow3+3.\left(4+3.3!\right)=69\) số
Xác suất: \(P=\dfrac{69}{180}=\dfrac{23}{60}\)

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là