Cho ti lệ thức a − 3 a + 3 = b − 6 b + 6 . Chứng minh a b = 1 2 ( a ≠ − 3 ; b ≠ − 6 )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
PT
1
CM
31 tháng 3 2018
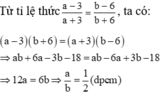
Từ tỉ lệ thức a − 3 a + 3 = b − 6 b + 6 ,ta có:
a − 3 b + 6 = a + 3 b − 6 ⇒ a b + 6 a − 3 b − 18 = a b − 6 a + 3 b − 18 ⇒ 12 a = 6 b ⇒ a b = 1 2 ( d p c m )
LM
1
KT
21 tháng 7 2018
\(\frac{a-3}{a+3}=\frac{b-6}{b+6}\) \(\Rightarrow\)\(\frac{a-3}{b-6}=\frac{a+3}{b+6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a-3}{b-6}=\frac{a+3}{b+6}=\frac{a-3+a+3}{b-6+b-6}=\frac{2a}{2b}=\frac{a}{b}\) (1)
\(\frac{a-3}{b-6}=\frac{a+3}{b+6}=\frac{a-3-a-3}{b-6-b-6}=\frac{-6}{-12}=\frac{1}{2}\) (2)
Từ (1) và (2) suy ra: \(\frac{a}{b}=\frac{1}{2}\)
LD
0
15 tháng 10 2017
bài 2
(bài này là đề thi olympic Toán,Ireland 1997),nhưng cũng dễ thôi
Giả sử ngược lại \(a^2+b^2+c^2< abc\)
khi đó \(abc>a^2+b^2+c^2>a^2\)nên \(a< bc\)
Tương tự \(b< ac,c< ab\)
Từ đó suy ra :\(a+b+c< ab+bc+ac\left(1\right)\)
mặt khác ta lại có:\(a^2+b^2+c^2\ge ab+bc+ac\)nên
\(abc>a^2+b^2+c^2\ge ab+bc+ac\)
\(\Rightarrow abc>ab+ac+bc\left(2\right)\)
Từ (1),(2) ta có\(abc>a+b+c\)(trái với giả thuyết)
Vậy bài toán được chứng minh
15 tháng 10 2017
3)để đơn giản ta đặt \(x=\frac{1}{a},y=\frac{1}{b},z=\frac{1}{c}\).Khi đó \(x,y,z>0\)
và \(xy+yz+xz\ge1\)
ta phải chứng minh có ít nhất hai trong ba bất đẳng thức sau đúng
\(2x+3y+6z\ge6,2y+3z+6x\ge6,2z+3x+6y\ge6\)
Giả sử khẳng định này sai,tức là có ít nhất hai trong ba bất đẳng thức trên sai.Không mất tính tổng quát,ta giả sử
\(2x+3y+6z< 6\)và \(2y+3z+6x< 6\)
Cộng hai bất đẳng thức này lại,ta được:\(8x+5y+9z< 12\)
Từ giả thiết \(xy+yz+xz\ge1\Rightarrow x\left(y+z\right)\ge1-yz\)
\(\Rightarrow x\ge\frac{1-yz}{y+z}\)Do đó
\(8\frac{1-yz}{y+z}+5y+9z< 12\Leftrightarrow8\left(1-yz\right)+\left(5y+9z\right)\left(y+z\right)< 12\left(y+z\right)\)
\(\Leftrightarrow5y^2+6yz+9z^2-12y-12z+8< 0\)
\(\Leftrightarrow\left(y+3z-2\right)^2+4\left(y-1\right)^2< 0\)(vô lý)
mâu thuẫn này chứng tỏ khẳng định bài toán đúng.Phép chứng minh hoàn tất.
