Gọi S là tập các giá trị nguyên của m để hàm số y = x + 2 m - 3 x - 3 m + 2 đồng biến trên khoảng - ∞ ; 14 . Tổng các phần tử của S bằng
A. -10
B. -9
C. -6
D. -5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

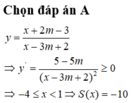

y′=−m2+2m+3(x−m)2′�=−�2+2�+3(�−�)2
Hàm số đồng biến →y′>0→�′>0
→−m2+2m+3>0→−�2+2�+3>0
↔−1<m<3↔−1<�<3
Vì m nguyên nên m� có 33 giá trị.

Đáp án C
Ta có y ' = − m 2 + 2016 m + 2017 x + m 2 , y ' = 0 đồng biến trên từng khoảng xác định nếu
y ' > 0 ∀ x ∈ D ⇔ − m 2 + 2016 m + 2017 > 0 ⇔ m ∈ − 1 ; 2017
Ta đếm số nguyên trong
− 1 ; 2017 thì có 2016 số nguyên trong đó.

Chọn đáp án B.
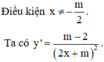
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364

Hàm bậc 2 có \(a=1>0;-\dfrac{b}{2a}=-\dfrac{m+1}{2}\) nên đồng biến trên \(\left(-\dfrac{m+1}{2};+\infty\right)\)
Để hàm đồng biến trên khoảng đã cho thì \(-\dfrac{m+1}{2}\le-2\Rightarrow m\ge3\)
\(\Rightarrow\) Tập đã cho có vô số phần tử
Còn phần tử nguyên thì có \(2021-3=2018\) phần tử