Một đoạn mạch gồm cuộn cảm có độ tự cảm L và điện trở thuần r mắc nối tiếp với tụ điện có điện dung C thay đổi được. Đặt vào hai đầu mạch một điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Khi điều chỉnh để điện dung của tụ điện có giá trị C = C 1 thì điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U, cường độ dòng điện trong mạch khi đó có biểu thức i 1 = 2 6 cos 100 πt + π 4 (A). Khi điều chỉnh để điện dung của tụ điện có giả trị C = C 2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại. Cường độ dòng điện tức thời trong mạch khi đó có biểu thức là
A. i 2 = 2 2 cos 100 πt + 5 π 12 A
B. i 2 = 2 3 cos 100 πt + 5 π 12 A
C. i 2 = 2 2 cos 100 πt + π 3 A
D. i 2 = 2 3 cos 100 πt + π 3 A


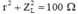
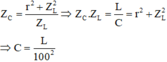
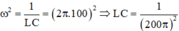
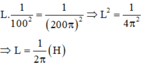
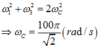
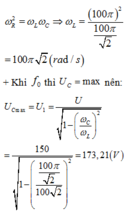
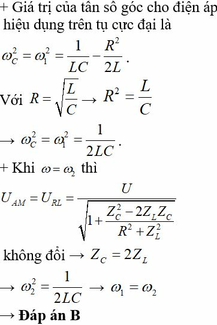
Đáp án A
+ Khi C = C 1 , ta có: điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U nên:
U d = U C = U ⇒ U r 2 + U L 2 = U C 1 = U 1 ⇒ r 2 + Z L 2 = Z C 1 = Z 1 2
Điện áp toàn mạch khi đó:
Thay vào (1), ta có:
U r 1 2 + U L 1 2 = U 2 = 4 U L 1 2 ⇒ U r 1 = 3 U L 1 ⇒ r = 3 Z L 4
Từ (2), (3), (4) ta có:
tanφ 1 = Z L − Z C 1 r = Z L − 2 Z L 3 Z L = − 1 3 ⇒ φ 1 = − π 6 ⇒ φ u = φ 1 + φ i 1 = − π 6 + π 4 = π 12 5
+ Khi C = C 2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại nên
Z C 2 = r 2 + Z L 2 Z L = 3 . Z L 2 + Z L 2 Z L = 2 Z L
Tổng trở của mạch khi đó:
Z 2 = r 2 + Z L − Z C 2 2 = 3 Z L 2 + Z L − 4 Z L 2 = 2 3 Z L
Độ lệch pha khi Z C = Z C 2 :
tanφ 2 = Z L − Z C 2 r = Z L − 4 Z L 3 Z L = − 3 ⇒ φ 2 = − π 3 ⇒ φ i 2 = φ u − φ 2 = π 12 − − π 3 = 5 π 12
+ Áp dụng định luật Ôm cho cả hai trường hợp ta có:
U = I 1 . Z 1 = I 2 . Z 2 ⇒ I 02 = I 01 . Z 1 Z 2 = 2 6 . 2 . Z L 2 3 . Z L = 2 2 A
+ Biểu thức cường độ dòng điện khi Z C = Z C 2 : i 2 = 2 2 cos 100 πt + 5 π 12 A