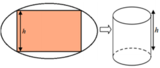
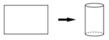
Người ta cần cắt một tấm tôn có hình dạng là một elip với độ dài trục lớn bằng 2a, độ dài trục bé bằng 2 b a > b > 0 để được một tấm tôn hình chữ nhật nội tiếp elip. Người ta gò tấm tôn hình chữ nhật thu được một hình trụ không có đáy (như hình bên). Tính thể tích lớn nhất có thể thu được của khối trụ đó.
A. 2 a 2 b 3 2 π
B. 2 a 2 b 3 3 π
C. 4 a 2 b 3 2 π
D. 4 a 2 b 3 3 π

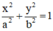
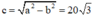 ⇒ F
⇒ F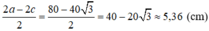
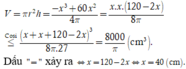
Đáp án B
Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ
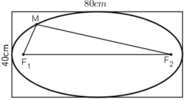
Chọ hệ trục tọa độ Oxy như hình vẽ với tứ giác ABCD là hình chữ nhật nối tiếp hình (E)
Gọi A x 0 ; y 0 x 0 > y 0 > 0 , khi đó ta có A B = 2 π R C D = h ⇔ 2 x 0 = 2 π R 2 y 0 = h ⇔ x 0 = π R y 0 = h 2
Thể tích khối trụ là V = π R 2 h = 2 x 0 2 π . y 0 mà A ∈ E ⇒ x 0 2 a 2 + y 0 2 b 2 = 1 ⇒ x 0 2 = a 2 b 2 b 2 − y 0 2