Gọi v 0 là vận tốc ban đầu của chuyển động. Công thức liên hệ giữa vận tốc v, gia tốc a và quãng đường s vật đi được trong chuyển động thẳng biến đổi đều là:
A. v + v 0 = 2 a s
B. v − v 0 = 2 a s
C. v 2 + v 0 2 = 2 a s
D. v 2 − v 0 2 = 2 a s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CT quãng đường đi dc của chuyển động nhanh dần đều là:
\(s=v_0t+\dfrac{1}{2}at^2\)(a với v0 cùng dấu)

Kí hiệu s = x − x 0 là quãng đường đi được từ thời điểm 0 đến thời điểm t ; v 0 là vận tốc ban đầu tại thời điểm t = o ; v là vận tốc tại thời điểm t;a là gia tốc của chuyển động. Công thức liên hệ: v 2 − v 0 2 = 2 a s .

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

Vật đã đi được 4s
\(v=9-2t\Rightarrow\left\{{}\begin{matrix}v_0=9\\a=-2\end{matrix}\right.\)
\(S=v_0t+\dfrac{1}{2}at^2=20m\)

Chọn D.
Từ công thức v = vo + at
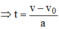
thế vào công thức:
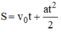
Ta được:
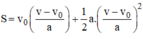
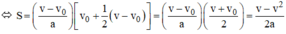
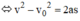

Chọn B.
Công thức liên hệ giữa vận tốc, gia tốc và quãng đường đi được của chuyển động thẳng nhanh dần đều:
v 2 - v 0 2 = 2 a s ⇒ v 2 = 2 a s + v 0 2

Chọn D.
Đối với chuyển động thẳng nhau dần đều , chọn chiều dương là chiều chuyển động: v 2 - v 0 2 = 2 a s
Chọn D