cho m và n là các số nguyên dương thỏa mãn m/n là phân số tối giản và phân số 4m+3n/5m+2n không tối giản
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
19 tháng 12 2015
Trong một số trường hợp, có thể sử dụng mối quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số nguyên dương a, b, đó là : ab = (a, b).[a, b], trong đó (a, b) là ƯCLN và [a, b] là BCNN của a và b. Việc chứng minh hệ thức này khụng khú :
Theo định nghĩa ƯCLN, gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1 (*)
Từ (*) => ab = mnd2 ; [a, b] = mnd
=> (a, b).[a, b] = d.(mnd) = mnd2 = ab
=> ab = (a, b).[a, b] . (**)
CM
6 tháng 10 2017
Chọn đáp án D.
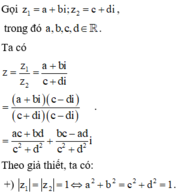
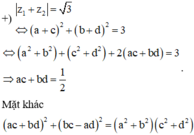
nên kết hợp với các đẳng thức ở trên, ta được
Tổng quát bài toán chúng ta có kết quả sau:
trong đó m, n, p là độ dài ba cạnh của một tam giác thì
PH
1
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
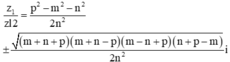
Đặt \(d=\left(3n+2,2n+7\right)\).
Suy ra \(\hept{\begin{cases}3n+2⋮d\\2n+7⋮d\end{cases}}\Rightarrow3\left(2n+7\right)-2\left(3n+2\right)=17⋮d\).
\(\Rightarrow\orbr{\begin{cases}d=1\\d=17\end{cases}}\)
Để \(\frac{3n+2}{2n+7}\)là phân số tối giản thì \(d\ne17\)do đó \(3n+2\ne17k\Leftrightarrow n\ne\frac{17k-2}{3}\left(k\inℤ\right)\).
