Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình cos 2 x + 3 sin x . cos x = 1
A. 3
B. 3 10 10
C. 3 10 5
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
27 tháng 11 2017
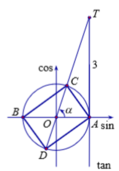
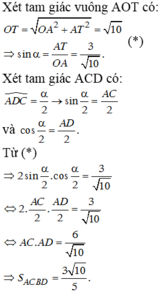
Đáp án B
Điều kiện: cos x ≠ 0 tan x ≠ 1
Ta có:
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + tan π 4 1 − tan x . tan π 4 = 1
⇔ tan x + tan x + 1 1 − tan x = 1 ⇔ tan x − tan 2 x + tan x + 1 = 1 ⇔ tan x = 0 tan x = 2 ⇔ x = k π x = arctan 2 + k π k ∈ ℤ
suy ra 4 nghiệm trên đường tròn lượng giác là x = 0 x = π và x = arctan 2 x = arctan 2 + π
Vậy diện tích cần tính là S = 0 , 948
HN
1 tháng 8 2021
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{cot\left(\dfrac{\pi}{4}+x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^4x\)
Giờ hạ bậc nữa là xong rồi. Làm nốt
HP
1 tháng 8 2021
Hình như đề bạn bị lỗi, thấy chỗ nào cũng ghi là \(cos^44x\).
ĐK: \(x\ne\dfrac{3\pi}{4}+k\pi;x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right).tan\left(\dfrac{\pi}{4}+x\right)}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{sin\left(\dfrac{\pi}{4}-x\right)}{cos\left(\dfrac{\pi}{4}-x\right)}.\dfrac{sin\left(\dfrac{\pi}{4}+x\right)}{cos\left(\dfrac{\pi}{4}+x\right)}}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{cosx-sinx}{cosx+sinx}.\dfrac{cosx+sinx}{cosx-sinx}}=cos^44x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^44x\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^24x=cos^44x\)
\(\Leftrightarrow cos^44x-\dfrac{1}{2}cos^24x-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^24x=1\\cos^24x=-\dfrac{1}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{2}cos8x=\dfrac{1}{2}\)
\(\Leftrightarrow cos8x=1\)
\(\Leftrightarrow x=\dfrac{k\pi}{4}\)
Đối chiều điều kiện ban đầu ta được \(x=\dfrac{k\pi}{2}\)
CM
17 tháng 3 2019
Đáp án D
Điều kiện cos x ≠ 0 cos x + π 4 ≠ 0
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + 1 1 − tan x − 1 = 0
⇔ − tan 3 x + 3 tan x 1 − tan x = 0 ⇔ tan x ≠ 1 tan x 3 − tan x = 0 ⇔ tan x = 0 tan x = 3
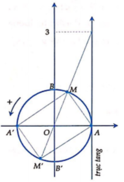
Ta có biểu thị các họ nghiệm của phương trình trẻn đường trọn lượn giác như hình bên.
Vậy đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình tan x + tan x + π 4 = 1 là tứ giác A M A ' M ' .
Cách 1: Đường thẳng có phương trình y = 3 x ⇔ 3 x − y = 0 .Khoảng cách từ điểm A 1 ; 0 đến M M ' là 3.1 − 0 3 2 + 1 2 = 3 10 . Do đó diện tích tứ giác A M A ' M ' là
S A M A ' M ' = 2 S A M M ' = 2. 1 2 . M M ' . d A , M M ' = 2. 3 10 ≈ 2.0,949
Cách 2: Ta có sin M O A ^ = 3 3 2 + 1 2 = 3 10
⇒ S A M A ' M ' = 4. S M O A = 4. 1 2 . O M . O A . sin M O A ^ = 2. 3 10 ≈ 2.0,949
Ta chọn D, do chỉ có 0,949 gần 2.0,949 nhất.
