Công thức tính thể tích V của khối cầu có bán kính bằng R là
A. V = 4 π R 2
B. V = 4 3 π R 2
C. V = 4 3 π R 3
D. V = π R 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 7 2018
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.
CM
28 tháng 2 2019
Chọn A.
Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.
Do đó thể tích khối trụ là:
V = πR 2 h = 2 πa 3
AM
17 tháng 1 2023
Thể tích của quả cầu thép là: \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi.\left(0,15\right)^3=0,0045\pi\left(m^3\right)\)
Khối lượng của quả cầu thép là: \(m=DV=7850.0,0045\pi\approx111\left(kg\right)\)
14 tháng 4 2022
\(C=2\cdot1.25\cdot3.142=3.142\cdot2.5=7,855\left(m\right)\)
14 tháng 4 2022
Chu vi của đường tròn là
C = 2 π R = 2 . ( 1,25) . 3,142 = 7,855 ( m)
VT
24 tháng 3 2017
Đáp án: D
Ta có: ZL = 60Ω; ZC = 20Ω
Tổng trở của mạch:
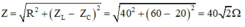
Biểu thức của i:
Ta có: u = 240√2cos100πt (V) → i = I0cos(100πt + φi)
Với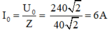 
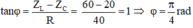
→ φ = φu – φi → φi = φu – φ = 0 – π/4 = – π/4 rad
Vậy i = 6cos(100πt – π/4) (A)
Đáp án C