Tìm tất cả các giá trị của tham số thực m để phương trình log 3 2 x - 3 log 3 x + 2 m - 7 = 0 có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) = 72.
A. m = 61 2
B. m = 3
C. K h ô n g t ồ n t ạ i
D. m = 9 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
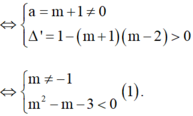
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
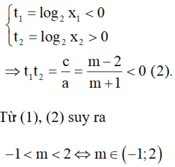

Đáp án D.
Đặt t = log 3 x ⇒ t 2 − 3 t + 2 m − 7 = 0
PT có 2 nghiệm khi Δ = 9 − 4 2 m − 7 = 37 − 8 m > 0 ⇒ PT có 2 nghiệm t 1 ; t 2 ⇒ log 3 x 1 = t 1 log 3 x 2 = t 2 ⇒ x 1 = 3 t 1 x 2 = 3 t 2
Khi đó theo định lý Viet ta có: t 1 + t 2 = 3 t 1 t 2 = 2 m − 7
Do:
x 1 + 3 x 2 + 3 = 72 ⇔ x 1 x 2 + 3 x 1 + x 2 = 63 ⇔ 3 t 1 .3 t 2 + 3 3 t 1 + 3 t 2 = 63 ⇔ 3 t 1 + t 2 + 3 3 t 1 + 3 t 2 = 63 ⇔ 3 t 1 + 3 t 2 = 12 ⇔ 3 3 − t 2 + 3 t 2 = 12
Đặt:
u = 3 t 2 ⇒ 27 u + u = 12 ⇔ u = 3 u = 9 ⇒ t 2 = 1 ⇒ t 1 = 2 t 2 = 2 ⇒ t 1 = 1 ⇒ t 1 t 2 = 2 ⇒ m = 9 2 t / m .

Đáp án B.
Đặt t = log 2 x , khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 ⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt ⇔ a = m + 1 ≠ 0 ∆ ' = 1 - m + 1 m - 2 > 0 ⇔ m ≠ - 1 m 2 - m - 3 < 0 1 .
Khi đó gọi x 1 ; x 2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x 1 < 1 < x 2 suy ra t 1 = log 2 x 1 < 0 t 2 = log 2 x 2 > 0 ⇒ t 1 t 2 = c a = m - 2 m + 1 < 0 2 .
Từ (1), (2) suy ra - 1 < m < 2 ⇔ m ∈ - 1 ; 2 là giá trị cần tìm.

Chị quản lí ơi để phương trình có 2 nghiệm phân biệt thì \(\Delta>0\)!
Quá dễ . số cần tìm là 10 . Đúng đấy , bài này mk làm rồi , chắc chắn 100% luôn !!!

Để phương trình 1 có 2 nghiệm phân biệt thì : \(\Delta>0\)
\(\Leftrightarrow\left(-4\right)^2-4\left(3-m\right)>0\\ \Leftrightarrow4+4m>0\\ \Leftrightarrow m>-1\circledast\)
Vì phương trình 1 cso hai nghiệm phân biệt
=> \(x_1=\dfrac{4-\sqrt{4+4m}}{2}\)
Theo bài ra ta có phương trình 1 cso 2 no phân biệt với \(x_1\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{4+4m}}{2}\le0\)
Mà ta có 2 > 0
\(\Rightarrow4-\sqrt{4+4m}\le0\\ \Leftrightarrow m\ge3\circledast\circledast\)
Từ * và ** thì với giá trị \(m\ge3\) thì bài toán được t/m
Đáp án D.
Đặt t = log3 x => t2 – 3t + 2m – 7 = 0
PT có 2 nghiệm khi ∆ = 9 - 4 2 m - 7 = 37 - 8 m > 0
=> PT có 2 nghiệm t1; t2
⇒ log 3 x 1 = t 1 log 3 x 2 = t 2 ⇒ x 1 = 3 t 1 x 2 = 3 t 2
Khi đó theo định lý Viet ta có:
t 1 + t 2 = 3 t 1 . t 2 = 2 m - 7
Do
Đặt