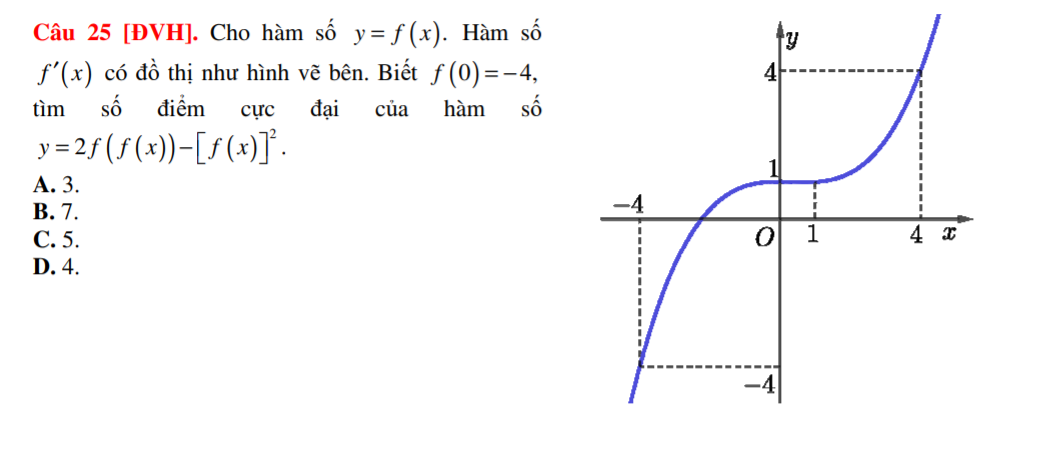
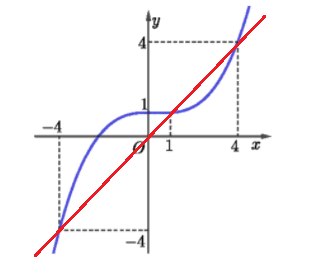
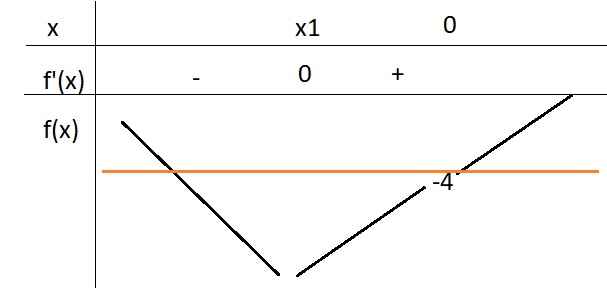
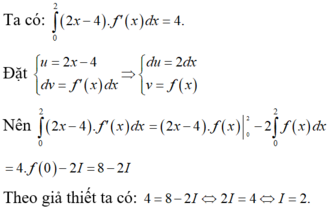Cho hàm số
f
(
x
)
=
x
2
+
4
-
2
x
2
k
h
i
x
≠
0
2
a
-
5
4
k
h
i
x
=
0
. Tìm giá trị thực của tham số ![]() để hàm số f(x) liên tục tại x=0.
để hàm số f(x) liên tục tại x=0.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.