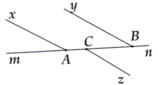
Cho hình vẽ bên, biết y B n ^ - 148 ° = m A x ^ = z C n ^ = 32 ° . Chứng minh ba đường thẳng Ax, By và Cz đôi một song song.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
22 tháng 11 2022
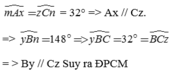
Bài 3:
\(\left\{{}\begin{matrix}x+y>=2\sqrt{xy}\\y+z>=2\sqrt{yz}\\x+z>=2\sqrt{xz}\end{matrix}\right.\Leftrightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)>=8xyz\)
Dấu = xảy ra khi x=y=z
NH
1
22 tháng 5 2020
a, Giả sử \(x,y \vdots 3\)
=> \(x^2 ;y^2 \) : 3 dư 1
=> \(z^2 = x^2+y^2 \) : 3 dư 2 ( vô lý vì \(z^2\) là số chính phương )
Vậy \(x\vdots 3y\vdots 3 => xy \vdots 3\)
Chứng minh tương tự \(xy \vdots 4\)
\((3;4) =1 => xy \vdots 12\)
20 tháng 2 2019
\(4x-xy+2y=3\)
\(\Rightarrow x\left(4-y\right)-8+2y=3-8\)
\(\Rightarrow x\left(4-y\right)-2\left(4-y\right)=-5\)
\(\Rightarrow\left(x-2\right)\left(4-y\right)=-5\)
\(\Rightarrow\left(x-2\right)\left(y-4\right)=5\)
\(\Rightarrow\left(x-2\right);\left(y-4\right)\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Tự xét bảng
\(3y-xy-2x-5=0\)
\(\Rightarrow y\left(3-x\right)-2x=5\)
\(\Rightarrow y\left(3-x\right)+6-2x=5+6\)
\(\Rightarrow y\left(3-x\right)+2\left(3-x\right)=11\)
\(\Rightarrow\left(y+1\right)\left(3-x\right)=11\)
\(\Rightarrow\left(3-x\right);\left(y+1\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Tự xét
\(2xy-x-y=100\)
\(\Rightarrow x\left(2y-1\right)-y=100\)
\(2x\left(2y-1\right)-\left(2y-1\right)=100+1\)
\(\left(2x-1\right)\left(2y-1\right)=101\)
\(\Rightarrow\left(2x-1\right);\left(2y-1\right)\inƯ\left(101\right)=\left\{\pm1;\pm101\right\}\)
Tự xét bảng
P/s : bài 3 có gì sai ko ?
28 tháng 4 2020
Bài 3 :
Áp dụng BĐT \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\Rightarrow\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
Ta có :
\(\frac{x}{x+1}=\frac{x}{x+x+y+z}=\frac{x}{\left(x+y\right)+\left(x+z\right)}\)
\(\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}\right)\)
Tương tự ta có:
\(\frac{y}{y+1}\le\frac{1}{4}\left(\frac{y}{x+y}+\frac{y}{y+z}\right)\)
\(\frac{z}{z+1}\le\frac{1}{4}\left(\frac{z}{x+z}+\frac{z}{y+z}\right)\)
\(\Rightarrow\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}\right)\)
\(+\frac{1}{4}\left(\frac{y}{x+y}+\frac{y}{y+z}\right)+\frac{1}{4}\left(\frac{z}{x+z}+\frac{z}{y+z}\right)\)
\(\Rightarrow\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}+\frac{y}{x+y}+\frac{y}{y+z}+\frac{z}{x+z}+\frac{z}{y+z}\right)\)
\(\Rightarrow\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\le\frac{1}{4}.6=\frac{3}{2}\)
