Cho biết 3 số hạng đầu của khai triển x + 1 2 x n , x > 0 có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên.
A. 35 8 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

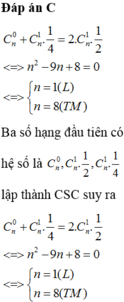
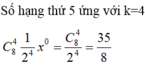

Chọn A
Theo đề bài ta có: ![]()
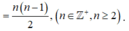 .
.
Lại theo tính chất của cấp số cộng có:
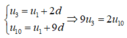
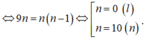
Khi đó số hạng tổng quát trong khai triển x - 1 x 2 10
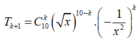
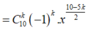
Số hạng không chứa x trong khai triển trên ứng với 
Vậy hệ số của số hạng không chứa x trong khai triển trên là ![]()

\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)

Ta có x + 1 x n = ∑ k = 0 n C n k x n - 2 k
Theo đề ta có C n 0 + C n 1 = 24 ⇔ 1 + n = 24 ⇔ n = 23
Số hạng chứa x mũ nguyên dương thỏa n - 2 k > 0 ⇔ k < n 2 = 23 2
Do k ∈ Z nên k ∈ 1 ; 2 ; 3 ; . . 11 .
Suy ra có 12 số hạng chứa x mũ nguyên dương
Đáp án C