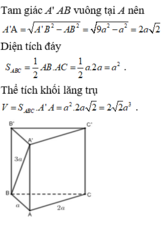
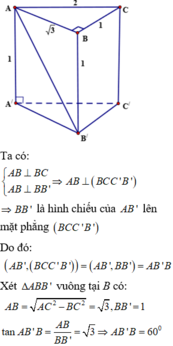
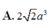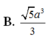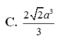Cho hình lăng trụ đứng A B C . A 1 B 1 C 1 có đáy ABC là tam giác vuông tại B, AB= 4, BC=6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh B B 1 , A 1 B 1 , B C . Thể tích của khối tứ diện C 1 K M N là
A. 15.
B. 5.
C. 45.
D. 10.