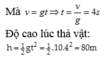Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g = 10 m / s 2 . Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thành Nam
28 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
VT
13 tháng 9 2017
Quãng đường vật rơi nửa thời gian đầu:
Quãng đường vật rơi nửa thời gian cuối
Quãng đường vật rơi: h = h 1 + h 2
VT
18 tháng 10 2017
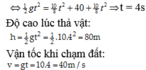
Đáp án D
Quãng đường vật rơi nửa thời gian đầu:
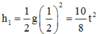
Quãng đường vật rơi nửa thời gian cuối
Quãng đường vật rơi:
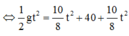
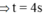
Độ cao lúc thả vật:
Vận tốc khi chạm đất:
v = gt = 10.4 = 40m/s
HD
Hà Đức Thọ
Admin
5 tháng 6 2018
Gọi thời gian rơi nửa quãng đường sau là \(t(s)\), thì thời gian rơi nửa quãng đường đầu là \(t+1\)
Theo đề bài ta có:
\(\dfrac{h}{2}=\dfrac{1}{2}.g.(t+1)^2\Rightarrow h = g(t+1)^2\) (1)
\(h=\dfrac{1}{2}.g.(t+t+1)^2\Rightarrow h=\dfrac{1}{2}.g.(2t+1)^2\) (2)
Từ (1) và (2) suy ra: \( g(t+1)^2 = \dfrac{1}{2}g.(2t+1)^2\)
\(\Rightarrow t^2+2t+1= \dfrac{1}{2}(4t^2+4t+1)\)
\(\Rightarrow t^2 = \dfrac{1}{2}\)
\(\Rightarrow t = \dfrac{1}{\sqrt 2}(s)\)
Suy ra:
Độ cao: \(h = g(t+1)^2=10.(\dfrac{1}{\sqrt 2}+1)^2\approx 29,1 (m)\)
Thời gian chạm đất: \(t_1= 2.t+1=\sqrt 2 + 1 \approx 2,41 (s)\)
Tốc độ khi chạm đất: \(v=g.t=10.2,41=24,1(m/s)\)
VT
10 tháng 10 2019
Đáp án A
Quãng đường vật rơi trong 3 giây đầu:
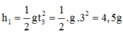
Quãng đường vật rơi trong 2 giây đầu:
Quãng đường vật rơi trong giây thứ 3:
Mà
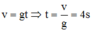
Độ cao lúc thả vật:
VT
29 tháng 1 2018
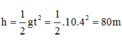
Quãng đường vật rơi trong 3 giây đầu:
Quãng đường vật rơi trong 2 giây đầu:
Quãng đường vật rơi trong giây thứ 3:
