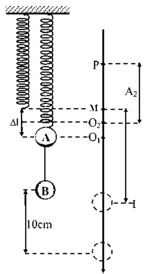
Một lò xo nhẹ có độ cứng 100 N/m, đầu trên treo vào một điểm cố định, đầu dưới gắn vào vật A có khối lượng 250 g; vật A được nối với vật B cùng khối lượng, bằng một sợi dây mềm, mảnh, nhẹ, không dãn và đủ dài. Từ vị trí cân bằng của hệ, kéo vật B thẳng đứng xuống dưới một đoạn 10 cm rồi thả nhẹ. Bỏ qua các lực cản, lấy giá trị gia tốc trọng trường g = 10 m / s 2 . Quãng đường đi được của vật A từ khi thả tay cho đến khi vật A dừng lại lần đầu tiên là
A. 19,1 cm
B. 29,1 cm
C. 17,1 cm
D. 10,1 cm




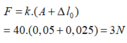


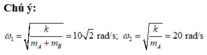
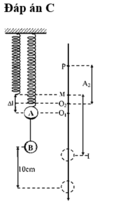








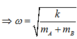
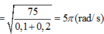

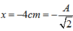
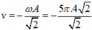

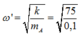

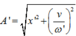
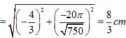


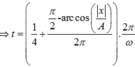
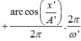


Đáp án A
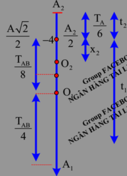
+ Độ giãn của lò xo tại vị trí cân bằng O của hệ hai vật Δ l 0 = 2 m g k = 5 cm, kéo hệ xuống dưới vị trí cân bằng 10 cm rồi thả nhẹ, vậy hệ sẽ dao động với biên độ A = 10 cm.
+ Ta có thể chia quá trình chuyển động của hệ thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật dao động điều hòa quanh vị trí cân bằng O.
· Tốc độ của hai vật khi đi qua vị trí cân bằng v m a x = ω A = k 2 m A = 100 2 cm/s.
Giai đoạn 2: Chuyển động của hai vật sau khi đi qua vị trí cân bằng O.
· Khi đi qua vị trí cân bằng O, tốc độ của vật A sẽ giảm, vật B sẽ chuyển động thẳng đứng lên trên với vận tốc ban đầu bằng v m a x , do có sự khác nhau về tốc độ nên hai vật không dao động chung với nhau nữa.
· Tuy nhiên sự kiện trên chỉ diễn ra rất ngắn, vật A ngay sau đó sẽ dao động quanh vị trí cân bằng mới ở phía trên O một đoạn 2,5 cm do đó ngay lập tức tốc độ của A sẽ tăng, trong khi B lại giảm → hệ hai vật lại được xem như ban đầu và dao động quanh vị trí cân bằng O.
Giai đoạn 3: Chuyển động của hai vật sau khi dây bị chùng
· Phương trình định luật II cho vật m 2 : m 2 g − T = m 2 a , khi T = 0 dây chùng → x = − g ω 2 = − 5 cm. Lúc này v A = 3 2 v m a x = 50 6 cm/s.
· Vật dao A dao động quanh vị trí cân bằng mới O' cách vị trí cân bằng cũ một đoạn Δ l = m g k = 2 , 5 cm với biên độ A ' = 2 , 5 2 + 50 6 20 2 = 6 , 61 cm.
Từ các lập luận trên ta thấy rằng khi A dừng lại lần đầu tiên ứng với vị trí biên trên, khi đó quãng đường vật đi được sẽ là S = 10 + 5 + (6,61 – 2,5) = 19,1 cm.