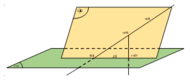
Cho mặt phẳng α và đường thẳng ∆ không vuông góc với α . Gọi u ∆ → , n α → lần lượt là vectơ chỉ phương của △ và vectơ pháp tuyến của α . Vectơ nào dưới đây là vectơ chỉ phương của △ ' là hình chiếu của △ trên α ?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.


Mặt phẳng
α
chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng
∆
là giao tuyến của
α
và
β
nên có VTCP ![]()
Theo giả thiết, ta có
u
∆
→
cùng phương với ![]()
Suy ra 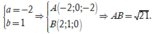
Chọn C.

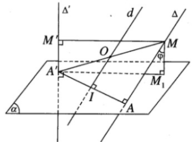
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.