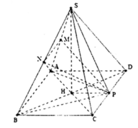
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên với đáy bằng 45 o . Gọi M, N, P lần lượt là trung điểm của SA, SB, CD. Thể tích khối tứ diện AMNP là ?
A. a 3 16
B. a 3 24
C. a 3 6
D. a 3 48
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
- Lập tỉ lệ thể tích khối tứ diện AMNP với khối chóp S.ABCD
- Tính thể tích khối chóp S.ABCD
- Tính thể tích khối tứ diện AMNP.
Cách giải:
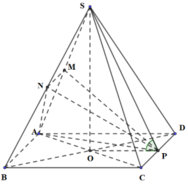

![]()


Đáp án B

Ta có: S B A ^ = 60 ∘ ⇒ S A = A B tan 60 ∘ = a 3
V A . A C D = 1 3 S A . S A C D = 1 3 . a 3 . a 2 2 = a 3 3 6
Lại có: V S . A M N V S . A C D = S M S C . S N S D = 1 4 ⇒ V S . A M N = a 3 3 24

Chọn đáp án C.
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O

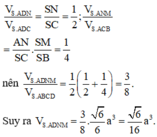


Chọn C.
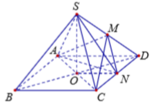
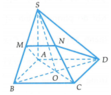
Gọi O là tâm mặt đáy, suy ra SO ⊥ (ABCD)
Góc giữa mặt bên và mặt đáy là S N O ^ = 60 °
![]()
Vì M là trung điểm của SD nên ![]()


Đáp án C
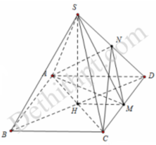
Ta có S C D ; A B C ^ = S M H ^ = 60 °
Khi đó S H = H M tan 60 ° = a 3
Mặt khác
S A C M = 1 2 A D . C M = 1 2 2 a . a = a 2
d N ; A C M = 1 2 S H = a 3 2 ⇒ V N . A C M = 1 3 d N ; A C M = a 3 3 6
Đáp án D
Hướng dẫn giải:
Gọi H là tâm của đáy khi đó S H ⊥ ( A B C D ) .
Dựng H P ⊥ C D .
Khi đó H P = a 2
Do vậy S A B P = a 2 2 ⇒ V S . A P B = a 3 12
Mặt khác V S . M N P V S . A B P = S M S A . S N S B . S P S P = 1 4
⇒ V S . M N P = a 3 48
Do vậy V A . M N P = V S . M N P = a 3 48 (do d(S;(MNP))=d(A;(MNP))).