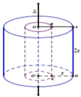
Một miếng giấy hình chữ nhật ABCD với A B = x , B C = 2 x và đường thẳng ∆ nằm trong mặt phẳng (ABCD), ∆ song song với AD và cách AD một khoảng bằng a, ∆ không có điểm chung với hình chữ nhật ABCD và khoảng cách từ A đến B đến ∆ . Tìm thể tích lớn nhất có thể có của khi quay hình chữ nhật ABCD quanh ∆ .
A. 64 π a 3 27 .
B. 64 π a 3 .
C. 63 π a 3 27 .
D. 64 π 27 .

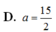


Đáp án A.
Ta có r 1 = O B = A O − A B = a − x
là bán kính đáy của khối trụ nhỏ.
Và r 2 = O A = a là bán kính đáy của
khối trụ lớn với chiều cao h = 2x
Suy ra thể tích cần tính là
V = V t l − V t n = π r 2 2 h − π r 1 2 h = 2 π x a 2 − a − x 2 = 2 π x 2 a x − x 2 ⇒ V = 2 π x 2 2 a − x = 8 π . x 2 . x 2 . 2 a − x ≤ 8 π . 8 a 3 27 = 64 π a 3 27 ⇒ V max = 64 π a 3 27 .