Tìm giá trị của m để đường thẳng (d): y = (2m – 5)x – 5m đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 3y = 7 và ( d 2 ): 3x + 2y = 13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2021
1.
\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)
Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)
\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)
2.
Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)
21 tháng 1 2023
Tọa độ giao điểm là:
4x-y=-7 và 2x-y=9
=>x=-8 và y=-25
Thay x=-8 và y=-25 vào (d), ta được:
-8(m+2)-2m-1=-25
=>-8m-16-2m-1=-25
=>-10m-17=-25
=>-10m=-8
=>m=4/5
3 tháng 1 2021
a) Để hàm số đồng biến thì a>0 => m-1>0 <=> m>1
b) Thay M(2;1) vào h/s
1=(m-1).2+2m-5 => m=2
3 tháng 1 2021
c) Để d song song với đường thẳng trên thì a=a' \(m-1=3\Leftrightarrow m=4\)
d) Cắt 1 điểm trên trục tung thì b=b' \(\Leftrightarrow2m-5=3\Leftrightarrow m=4\)
1 tháng 12 2017
a, pt hoanh độ giao điểm cua 2 đg thẳng d1 và d2 la: 2x - 5 = 1 <=> x = 3
vậy tọa độ giao điểm cua d1 va d2 la A(3;1)
Để d1 , d2, d3 đồng quy thì d3 phải đi qua diem A(3;1)
Ta co pt: (2m - 3).3 - 1 = 1
<=> 6m - 9 -1 = 1
<=> 6m = 11 <=> m = 11/6
mấy bài còn lại tương tự nha
Gọi I là giao điểm của ( d 1 ) và ( d 2 ). Khi đó tọa độ của I là nghiệm của hệ phương trình: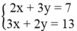
Tọa độ điểm I là I(5; -1)
Đường thẳng (d): y = (2m – 5)x – 5m đi qua I(5; -1) nên tọa độ của I nghiệm đúng phương trình đường thẳng:
Ta có: -1 = (2m – 5).5 – 5m ⇔ -1 = 10m – 25 – 5m
⇔ 5m = 24 ⇔ m = 24/5
Vậy với m = 24/5 thì đường thẳng (d) đi qua giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).