Một ôtô có khối lượng 1 tấn đang chuyển động với v = 54 k m / h thì tắt máy, hãm phanh, chuyển động chậm dần đều. Biết độ lớn lực hãm 3000N. Xác định quãng đường xe đi được cho đến khi dừng lại.
A. 18,75 m.
B. 486 m.
C. 0,486 m.
D. 37,5 m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
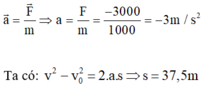

Ta có: v=54km/h=15m/s
Chọn chiều (+) là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
Theo định luật II - Niutơn, ta có:
a → = F → m → a = − F m = − 3000 1000 = − 3 m / s 2
Mặt khác, ta có: v 2 − v 0 2 = 2 as
↔ 0 − 15 2 = 2. ( − 3 ) s → s = 37 , 5 m
Đáp án: A

Đáp án B.
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
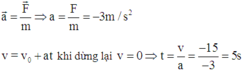

Chọn đáp án C
? Lời giải:
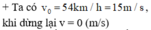
+ Chọn chiều dương là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh. Theo định luật II Newton F → h = m a →


Đáp án D.
Gọi v0 là vận tốc ban đầu của quãng đường đi 2s cuối. Ta có:
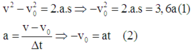
Từ (1) và (2) ta có: a = -0,9 m/s2
=> F = m.a = -450N. Dấu “-“ chứng tỏ lực ngược chiều chuyển động (lực hãm).

Ta có v 2 − v 0 2 = 2 as ↔ − v 0 2 = 2 as=3,6a (1)
Mặt khác a = v − v 0 Δ t → − v 0 = a t = 2 a (2)
Từ (1) và (2) ta suy ra:a=−0,9m/s2
Lực hãm phanh tác dụng lên ôtô:F=m.a=−450N
Đáp án: C

\(v_0=72\)km/h=20m/s
Gia tốc xe: \(v^2-v^2_0=2aS\)
\(\Rightarrow a=\dfrac{v^2-v^2_0}{2S}=\dfrac{0-20^2}{2\cdot40}=-5\)m/s2
Ta có: \(-F_{hãm}-F_{ms}=m\cdot a\)
\(F_{hãm}=-F_{ms}-m\cdot a=-\mu mg-m\cdot a=-0,2\cdot1000\cdot10-1000\cdot\left(-5\right)=3000N\)
Chọn D
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
Ta có: