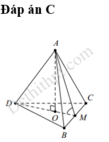
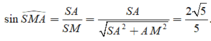Cho tứ diện đều ABCD. Gọi
φ
là góc giữa hai mặt phẳng (BCD) và (ABC) Khẳng định nào sau đây là đúng? ...
Đọc tiếp
Cho tứ diện đều ABCD. Gọi φ là góc giữa hai mặt phẳng (BCD) và (ABC) Khẳng định nào sau đây là đúng?
K
Khách
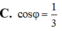
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
CM
14 tháng 3 2017
Đáp án C
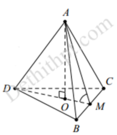
Gọi M là trung điểm của
B C ⇒ A M ⊥ B C D M ⊥ B C ⇒ B C ⊥ A D M
Suy ra
A B C ; D B C ^ = A M ; D M ^ = A D M ^ = φ
Gọi O là hình chiếu của A lên
mặt phẳng B C D
⇒ O là trọng tâm của tam giác BCD
⇒ O M = D M 3 = 1 3 . a 3 2 = a 3 6
Tam giác AMO vuông tại O, có
cos A M D ^ = O M A M = a 3 6 : a 3 2 = 1 3
Vậy cos φ = 1 3
CM
11 tháng 11 2019
Đáp án C
Hạ AH ^ (BCD) và HE ^ CD thì A E H ^ = α
Đặt AB = a ta tính được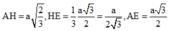 
CM
25 tháng 3 2019
Đáp án B
Ta có ngay B sai, góc giữa (ABD) và (ADC) không nhất thiết phải bằng
90
°
CM
21 tháng 9 2018
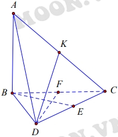
Chọn D.
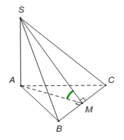
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
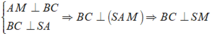
Do đó
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
