Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đo 1 2 n < 1 100 ⇔ n < log 1 2 1 100 ⇒ n ≥ 7 .
Ta cần gieo ít nhất 7 lần
a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4
Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với 
⇒ 
⇒ 
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
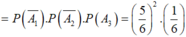
Lời giải:
Xác suất để xu 1 ngửa: $\frac{1}{2}$
Xác suất để xu 2 ngửa: $\frac{1}{2}$
Xác suất để xu 3 ngửa: $\frac{1}{2}$
Xác suất để 3 mặt cùng ngửa: $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}$
b. Biến cố C: “ Có ít nhất hai đồng tiền xuất hiện mặt ngửa” tức là có thể có hai hoặc ba đồng tiền xuất hiện mặt ngửa. Vì vậy chọn phương án B
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
Ta cần gieo ít nhất 7 lần.