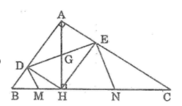
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tính diện tích tứ giác DENM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2020
Bài này hơi khó nên không chắc nhé bạn ==*
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE ( tính chất hình chữ nhật )
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
AH2 = HB . HC = 4 . 9 = 36 => AH = 6 ( cm )
Vậy DE = 6 ( cm )
b. *Gọi G là giao điểm của AH và DE
Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)
Suy ra tam giác GHD cân tại G
Ta có : \(\widehat{GDH}=\widehat{GHD}\left(1\right)\)
\(\widehat{GDH}+\widehat{MDH}=90^o\left(2\right)\)
\(\widehat{GHD}+\widehat{MHD}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : \(\widehat{MDH}=\widehat{MHD}\left(4\right)\)
\(\Rightarrow\Delta MDH\)cân tại M \(\Rightarrow MD=MH\left(5\right)\)
Ta lại có : \(\widehat{MDH}+\widehat{MDB}=90^o\left(6\right)\)
\(\widehat{MBD}+\widehat{MHD}=90^o(\Delta BHD\)vuông tại D ) ( 7 )
Từ (4) (6) và (7) , suy ra : \(\widehat{MDB}=\widehat{MBD}\)
\(\Rightarrow\Delta MDH\)cân tại M \(\Rightarrow MB=MD\left(8\right)\)
Từ (5) và (8) , suy ra : \(MB=MH\)hay M là trung điểm của BH
*\(\Delta GHE\)cân tại G
Ta có : \(\widehat{GHE}=\widehat{GEH}\left(9\right)\)
\(\widehat{GHE}+\widehat{NHE}=90^o\left(10\right)\)
\(\widehat{GEH}+\widehat{NEH}=90^o\left(11\right)\)
Từ (9) (10) và (11) , suy ra : \(\widehat{NHE}=\widehat{NEH}\left(12\right)\)
\(\Rightarrow\Delta NEH\)cân tại N => NE = NH ( 13 )
Lại có : \(\widehat{NEC}+\widehat{NEH}=90^o\left(14\right)\)
\(\widehat{NHE}+\widehat{NCE}=90^o(\Delta CEH\)vuông tại E ) ( 15 )
Từ (12) (14) và (15) , suy ra : \(\widehat{NDC}=\widehat{NCE}\)
Suy ra tam giác NCE cân tại N ⇒ NC = NE (16)
Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.
c. Tam giác BDH vuông tại D có DM là đường trung tuyến nên :
\(DM=\frac{1}{2}BH=\frac{1}{2}.4=2\left(cm\right)\)
\(\Delta CEH\)vuông tại E có EN là đường trung tuyến nên :
\(EN=\frac{1}{2}CH=\frac{1}{2}.9=4,5\left(cm\right)\)
Mà \(MD\perp DE\)và \(NE\perp DE\)nên MD // NE
Suy ra tứ giác DENM là hình thang
Vậy : \(S_{DENM}=\frac{DM+NE}{2}.DE=\frac{2+4,5}{2}.6=19,5\left(cm^2\right)\)
CM
16 tháng 9 2019
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
A H 2 = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)
Vậy DE = 6 (cm)
23 tháng 8 2021
b: Ta có: BC=BH+HC
nên BC=4+9
hay BC=13cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}cm\\AC=3\sqrt{13}cm\end{matrix}\right.\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{3\sqrt{13}}{13}\)
\(\cos\widehat{ABC}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\)
\(\tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
\(\cot\widehat{ABC}=\dfrac{AB}{AC}=\dfrac{2}{3}\)
23 tháng 8 2021
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}cm\\AC=3\sqrt{13}cm\end{matrix}\right.\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{3\sqrt{13}}{13}\)
\(\cos\widehat{ABC}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\)
\(\tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
\(\cot\widehat{ABC}=\dfrac{AB}{AC}=\dfrac{2}{3}\)
CM
6 tháng 8 2019
Theo chứng minh trên, ta có:
DM = MH = 1/2 BH = 1/2.4 = 2(cm)
EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)
DE = AH = 6(cm)
DENM là hình thang vuông, do đó diện tích của nó là:
S D E N M = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5( c m 2 ).
1 tháng 9 2021
a, Xét tam giác AHB vuông tại H, đường cao MH
\(AH^2=AM.AB\)( hệ thức lượng ) (1)
Xét tam giác AHC vuông tại H, đường cao HN
\(AH^2=AN.AC\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra : \(AM.AB=AN.AC\)(3)
b, Xét tam giác AMN và tam giác ACB ta có :
^A _ chung
\(\left(3\right)\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )
\(\frac{MN}{BC}=\frac{AM}{AC}\)(4)
Ta có : BC = HB + HC = 9 + 4 = 13 cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=9.13=117\Rightarrow AC=3\sqrt{13}\)cm
Theo định lí Pytago : \(AB=\sqrt{BC^2-AC^2}=\sqrt{169-\left(3\sqrt{13}\right)^2}=2\sqrt{13}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{2\sqrt{13}.3\sqrt{13}}{13}=6\)cm
lại có : \(AH^2=AM.AB\)cma => \(AM=\frac{36}{2\sqrt{13}}=\frac{18\sqrt{13}}{13}\)cm
Thay vào (4) ta được : \(\frac{MN}{13}=\frac{\frac{18\sqrt{13}}{13}}{3\sqrt{13}}=6\)cm
c, Lại có : \(AH^2=AN.AC\)cma => \(AN=\frac{36}{3\sqrt{13}}=\frac{12\sqrt{13}}{13}\)cm
Ta có : \(S_{AMN}=\frac{1}{2}AN.AM=\frac{1}{2}.\frac{12\sqrt{13}}{13}.\frac{18\sqrt{13}}{13}=\frac{108}{13}\)cm 2
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.2\sqrt{13}.3\sqrt{13}=39\)cm 2
Do \(S_{AMN}+S_{BMNC}=S_{ABC}\Rightarrow S_{BMNC}=S_{ABC}-S_{AMN}\)
\(=39-\frac{108}{13}=\frac{399}{13}\)cm2
Tam giác BDH vuông tại D có DM là đường trung tuyến nên: