Tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC
Tính tổng ∠ AEB + ∠ BCD bằng 2 cách:
Cách 1: Sử dụng kết quả ở câu b
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
18 tháng 2 2018
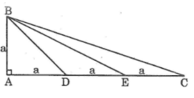
Qua E kẻ đường thảng song song với AC cắt tia BA tại F.
Ta có: FE//AD; AF//DE => AD=FE; AF=DE (Tcđoạn chắn) Mà AD=DE => AD=DE=FE=AF
FE//AC; AC vuông góc AB => FE vuông góc AB => ^BFE = 900
AB=a; AC=3a; AD=a (D thuộc AC); AD=AF => AB+AF=2a=BF; DC=3a-a=2a=CD
=> BF=CD
Xét tam giác BFE và tam giác CDE: EF=ED; ^BFE=^CDE=900; BF=CD
=> Tam giác BFE= Tam giác CDE (c/g/c)
=> BE=EC và ^BEF=^CED.
thấy ^BEF+^BED=900 => ^CED+^BED=^BEC=900
Xét tam giác BEC: BE=EC; ^BEC=900 => Tam giác BEC vuông cân tại E
=> ^BCE=450.
MH
5 tháng 5 2022
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=8^2+6^2=100\Rightarrow BC=10\left(cm\right)\)
b) Do \(AD=AB\) nên \(CA\) là trung tuyến
Mà \(AC\cap BK=E\) với \(BK\) là trung tuyến
\(\Rightarrow E\) là trọng tâm \(\Delta BCD\)
\(\Rightarrow CE=\dfrac{2}{3}AC=\dfrac{2}{3}.6=4\left(cm\right)\Rightarrow AE=2\left(cm\right)\)
c) Ta có \(CA\) vừa là trung tuyến vừa là đường cao \(\Delta BCD\)
\(\Rightarrow\Delta BCD\) cân tại \(C\Rightarrow CB=CD\)
