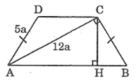
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a
Tính chiều cao của hình thang ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 3 2017
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
A B 2 = B C 2 + A C 2 = 5 a 2 + 12 a 2 = 169 a 2
16 tháng 7 2017
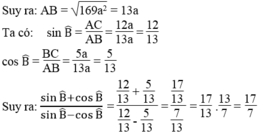
a,\(\frac{sinB+cosB}{sinB-cosB}=\frac{\frac{sinB}{cosB}+\frac{cosB}{cosB}}{\frac{sinB}{cosB}-\frac{cosB}{cosB}}=\frac{tanB+1}{tanB-1}\) (1)
doABCD co AD=BC=5a
nen trong tam giac vuong ABC co \(tanB=\frac{12a}{5a}=\frac{12}{5}\)
thay vao (1) ta co\(\frac{\sin B+\cos B}{\sin B-\cos B}=\frac{\tan B+1}{\tan B-1}=\frac{\frac{12}{5}+1}{\frac{12}{5}-1}=\frac{17}{7}\)
b, áp dụng đl pitago vào tam giác vuông ABC có \(AB^2=AC^2+CB^2\Rightarrow AB=13a\)
áp dụng hệ thức lượng vào tam giác vuông ABC \(CH\cdot AB=AC\cdot AB\Rightarrow CH=\frac{12\cdot5}{13}=\frac{60}{13}\)
24 tháng 7 2017
a, \(\Delta ABC\) có \(\widehat{C}=90^o\).
Áp dụng pytago có: \(AB=\sqrt{AC^2+BC^2}=\sqrt{\left(12a\right)^2+\left(5a\right)^2}=13a\)
\(\Delta ABC\) có \(\widehat{C}=90^o\)\(\Rightarrow\)\(\left\{{}\begin{matrix}\sin B=\dfrac{AC}{AB}=\dfrac{12a}{13a}=\dfrac{12}{13}\\cosB=\dfrac{BC}{AB}=\dfrac{5a}{13a}=\dfrac{5}{13}\end{matrix}\right.\)
Ta có: \(\dfrac{sinB+cosB}{sinB-cosB}=\dfrac{\dfrac{12}{13}+\dfrac{5}{13}}{\dfrac{12}{13}-\dfrac{5}{13}}=\dfrac{\dfrac{17}{13}}{\dfrac{7}{13}}=\dfrac{17}{7}\)
b, Có SABCD= \(\dfrac{CH.AB}{2}=\dfrac{CB.AC}{2}\Rightarrow CH.AB=BC.AC\Rightarrow CH=\dfrac{AC.BC}{AB}=\dfrac{12a.5a}{13a}=\dfrac{60a}{13}\approx4,615a\)
TN
22 tháng 10 2016
a) Có AD=BC=5a, AC=12a
Xét tam giác ABC vuộng tại C=> AB^2 =169a^2 <=> AB= 13a ( đlý Pitago )
Xét tam giác ABC vuộng tại C, có: SinABC =12a/13a, CosABC= 5a/13a
=> ( sin B + cosB )/ (sinB -cosB) = ( 12a/13a + 5a/13a)/(12a/13a - 5a/13a)= 17/7
b) Trong tam giác ADC, Kẻ AH vuông góc DC
Trong tam giác ACB, Kẻ CK vuông góc AB
Có AB//DC ( t/c hình thang)
mà AD vuông góc DC
=> AD vuông góc AB (1)
Tương tự có CK vuông góc DC (2)
(1)(2) => tứ giác ABCD là hcn ( dhnb hcn)
=> AD=CK
Xét tam giác ABC vuông tại C có CK là đường cao AB
<=> AB.CK= CB.CA
=> 13a.CK = 5a.12a
<=> CK= (60/13)a = AH
Xét tam giác AHC vuông tại H có HC= (144/13)a ( pitago)
Xét tam giác AHD vuông tại H có HD= (25/13)a ( pitago)
Mà H nằm giữa DC => DC = HC + HD = 13a
=> S ABCD= 1/2AH(AB+CD)= 1/2. (60/13)a. (13a +13a)= 60 a^2 (đvdt)
Chúc bạn học tốt!!!!!!
