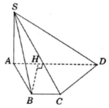
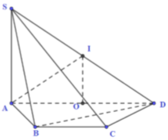
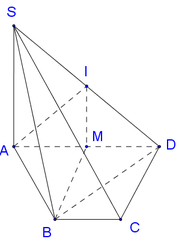
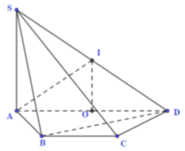
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh đáy AD và BC. AD = 2a,AB = BC = CD = a, B A D ⏞ = 60 o . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SD tao với mặt phẳng (ABCD) góc 45 o . Tính theo a thể tích V của khối chóp S.ABCD ?
A. V = a 3 3 6 .
B. V = a 3 3 2 .
C. V = 3 a 3 3 2 .
D. V = a 3 3 .


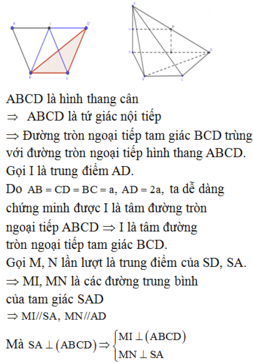








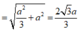
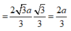
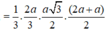
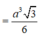
Đáp án B.
Hướng dẫn giải:Ta có
Suy ra tam giác SAD vuông cân tại A nên SA = AD =2a .
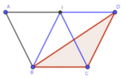
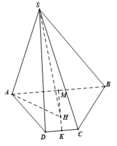
Trong hình thang ABCD , kẻ B H ⊥ A D ( H ∈ A D ) .
Do ABCD là hình thang cân nên A H = A D - B C 2 = a 2 .
Tam giác AHB ,có B H = A B 2 - A H 2 = a 3 2
Diện tích S A B C D = 1 2 ( A D + B C ) . B H = 3 a 3 2 4 .
Vậy V S . A B C D = 1 3 S A B C D . S A = a 3 3 2