Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
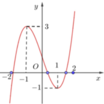
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Dựa vào bảng biến thiên ta suy ra đường thẳng y = - 2018 cắt đồ thị hàm số tại 2 điểm

Dễ nhận thấy hàm số có một điểm cực trị là điểm cực tiểu tại x = 1
Xét hàm số f(x) trên khoảng 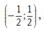 ta có: f(x) < f(0) với mọi
ta có: f(x) < f(0) với mọi 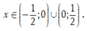
Suy ra x = 0 là điểm cực đại của hàm số.
Vậy hàm số có 2 điểm cực trị. Chọn C.

Hàm số y=f(x) liên tục trên ℝ và đồ thị hàm số đổi chiều tại hai điểm x=0;x=1 nên hàm số y=f(x) có hai điểm cực trị.
Chọn đáp án D.
Đáp án B