Cho hình vuông ABCD. Gọi I, K theo thứ tự là trung điểm của các cạnh AB, CD. Nối CI, AK. CMR: a) Tứ giác AICK là hình bình hành. b) Gọi M là trung điểm của BC. Gọi P, Q lần lượt là giao điểm của DM với IC và AK. CMR: DM = AK và DM vuông AK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2016
a,Xet tam giac ABC co :
AM=MB va BN=NC
=> MN la dtb => MN=1/2AC va MN//AC (1)
Xet tam giac ADC co :
DQ=QA va DP=PC
=> QP la dtb => QP=1/2AC va MN//AC (2)
Từ (1)(2) suy ra : MN=QP và MN//QP (phụ với AC)
Hay tu giac MNPQ la HBH
b, Xet tu giac MDPB co :
AB//DC=>MB//DP
AB=DC mà AM=MB va DP=PC
=> MB=DP
Hay tu giac MDPB la HBH
c, mk k bt lm xl bn
9 tháng 12 2018
a,Xet tam giac ABC co :
AM=MB va BN=NC
=> MN la dtb => MN=1/2AC va MN//AC (1)
Xet tam giac ADC co :
DQ=QA va DP=PC
=> QP la dtb => QP=1/2AC va MN//AC (2)
Từ (1)(2) suy ra : MN=QP và MN//QP (phụ với AC)
Hay tu giac MNPQ la HBH
b, Xet tu giac MDPB co :
AB//DC=>MB//DP
AB=DC mà AM=MB va DP=PC
=> MB=DP
Hay tu giac MDPB la HBH
29 tháng 10 2021
a: Xét tứ giác AICK có
AK//CI
AK=CI
Do đó: AICK là hình bình hành
CM
7 tháng 1 2017
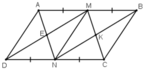
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;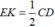 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
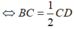
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
11 tháng 11 2018
MỌI NGƯỜI GIÚP MÌNH TRONG HÔM NAY VỚI Ạ !!! MAI MÌNH KIỂM TRA RÙI !!! THANK KIU EVERYONE, MONG NHẬN ĐK CÂU TRẢ LỜI SỚM ( MÀ MỌI NGƯỜI KHÔNG CẦN VX HÌNH ĐÂU Ạ ^^)
TD
11 tháng 11 2018
1) a. xét trong tam giác ABC có
I trung điểm AB và K trung điểm AC =>IK là đường trung bình của tam giác ABC=>IK song song với BC
vậy BCKI là hình thang (vì có hai cạng đáy song song)
b.
IK // và =1/2BC (cm ở câu a) =>IK song song NM
M trung điểm HC và N trung điểm HB mà HB+HC=CB =>MN=IK=1/2BC
suy ra MKIN là hbh => có hai đường chéo bằng nhau =>IM=NK
17 tháng 10 2020
đầu bài chỗ " đường chéo BD cắt AE" chắc là " đường chéo BD cắt AI" phải không bn???
a) ta có: AB = CD ( ABCD là h.b.h)
=> AK = IC \(\left(=\frac{1}{2}AB=\frac{1}{2}CD\right)\)
mà AK // IC
=> AKCI là hình bình hành ( dấu hiệu)
xét \(\Delta DFC\)
có: DI =IC (gt)
EI // FC ( AKCI là h.b.h)
=> EI là đường trung bình của \(\Delta DFC\)
=> DE = EF ( t/c')
cmtt với \(\Delta AEB\)ta có: EF = FB
=> DE=EF=FB
b) xét \(\Delta ABD\)
có: AM=MD
AK=KB
=> KM là đường trung bình của \(\Delta ABD\)
=> KM // BD và \(KM=\frac{1}{2}BD\)
cmtt với \(\Delta BCD\)ta có: IN//BD và \(IN=\frac{1}{2}BD\)
=> KM // IN (//BD)
\(KM=IN\left(=\frac{1}{2}BD\right)\)
=> KMIN là hình bình hành ( dấu hiệu)
11 tháng 4 2023
a: Xét tứ giác BMDP có
BM//DP
BM=DP
=>BMDP là hình bình hành
b: Xet ΔADH có P là trung điểm của AD và PQ//DH
=>Q là trung điểm của AH
ΔABP=ΔDAN
=>góc ABP=góc DAN
=>góc ABP+góc BAQ=90 độ
=>ΔABQ vuông tại Q
=>BQ vuông góc AH
=>ΔBAH cân tại B
=>BA=BH
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành