Tìm tập hợp các giá trị thực của m sao cho bất phương trình log 2 x + m ≥ 1 2 x 2 có nghiệm x ∈ 1 ; 3
A. 1 ln 2 ; + ∞
B. 9 2 − log 2 3 ; + ∞
C. 1 2 ; + ∞
D. 1 ln 2 + 1 2 log 2 ln 2 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Bất phương trình
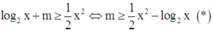
Xét hàm số
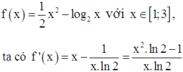
Phương trình
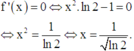
Tính các giá trị
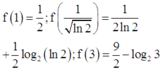
Dựa vào BBT, suy ra giá trị nhỏ nhất của hàm số f(x) là
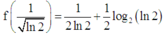
Khi đó, bất phương trình (*) có nghiệm
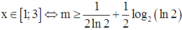

Bất phương trình x2-3x+2 ≤ 0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1 ≥ 0
![]()
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 , 1 ≤ x ≤ 2
Có f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

Giải bất phương trình x2- 3x+ 2≤ 0 ta được 1≤x≤2.
Bất phương trình mx2+ (m+ 1) x+ m+1≥0
⇔ m ( x 2 + x + 1 ) ≥ - x - 2 ⇔ m ≥ - x - 2 x 2 + x + 1
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 với 1≤ x≤ 2
Có đạo hàm f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 , ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
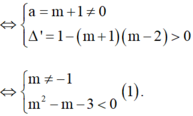
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
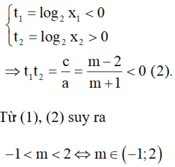

Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)
Đáp án D
Bất phương trình
log 2 x + m ≥ 1 2 x 2 ⇔ m ≥ 1 2 x 2 − log 2 x * .
Xét hàm số f x = 1 2 x 2 − log 2 x với x ∈ 1 ; 3 ,
ta có f ' x = x − 1 x . ln 2 = x 2 . ln 2 − 1 x . ln 2 .
Phương trình
f ' x = 0 ⇔ x 2 . ln 2 − 1 = 0 ⇔ x 2 = 1 ln 2 ⇔ x = 1 ln 2 .
Tính các giá trị
f 1 = 1 2 ; f 1 ln 2 = 1 2 ln 2 + 1 2 log 2 ln 2 ; f 3 = 9 2 − log 2 3.
Dựa vào BBT, suy ra giá trị nhỏ nhất của hàm số f(x) là
f 1 ln 2 = 1 2 ln 2 + 1 2 log 2 ln 2 .
Khi đó, bất phương trình (*) có nghiệm
x ∈ 1 ; 3 ⇔ m ≥ 1 2 ln 2 + 1 2 log 2 ln 2 .