Cho biết chu kì chuyển động của Mặt Trăng quanh Trái Đất là 27,32 ngày và khoảng cách từ Trái Đất đến Mặt Trăng là 3,84. 10 8 m. Hãy tính khối lượng của Trái Đất Giả thiết quỹ đạo của Mặt Trăng là tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1 tháng 12 2019
Khi Mặt Trăng chuyển động tròn quanh Trái Đất thì lực hấp dẫn giữa Mặt Trăng và Trái Đất đóng vai trò là lực hướng tâm, nên:
F h d = F h t ⇔ G m M r 2 = m v 2 r ⇔ G M r = v 2
Mà: v = ω r = 2 π T r
⇒ G M r = 4 π 2 T 2 r 2 ⇒ M = 4 π 2 r 3 T 2 G = 4 π 2 . ( 3 , 84.10 8 ) 3 ( 27 , 32.86400 ) 2 .6 , 67.10 − 11 ≈ 6.10 24 kg
Đáp án: B
VT
4 tháng 3 2019
Chọn đáp án A
Ta có :
T = 27,32 ngày = 2360448s
Lực hấp dẫn đóng vai trò là lực hướng tâm:
15 tháng 11 2018
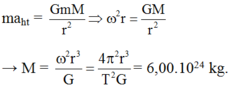
tốc độ gốc của mặt trăng
\(\omega=\dfrac{T}{2\pi}\)\(\approx2,66.10^{-6}\) (rad/s)
gọi m là khối lượng của mặt trăng, M là khối lượng của trái đất
vì mặt trăng chuyển động xung quanh trái đất
Fht=Fhd
\(\omega^2.R.m=\dfrac{G.m.M}{R^2}\Rightarrow M\approx\)6,01.1024kg
15 tháng 11 2021
\(a_{ht}=\omega^2r=\left(\dfrac{2\pi}{T}\right)^2r=\left(\dfrac{2\pi}{27,32.24.3600}\right)^2.3,84.10^5.10^3=2,7.10^{-3}\left(m\backslash s^2\right)\)
15 tháng 11 2021
\(R=3,84\cdot10^5km\)
\(T=27,32\) ngày= \(27,32\cdot24\cdot3600=2360448s\)
Tốc độ góc:
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{2360448}=2,66\cdot10^{-6}\)rad/s
Gia tốc:
\(a=r\cdot\omega^2=3,84\cdot10^5\cdot1000\cdot\left(2,66\cdot10^{-6}\right)^2=2,72\cdot10^{-3}\)m/s2
Gọi M và m lần lượt là khối lượng của Trái Đất và của Mặt Trăng, r là bán kính quỹ đạo của Mặt Trăng
Thay ω = 2 π /T vào ta được