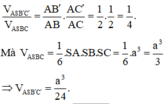ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
6 tháng 1 2019
Cho khối S.ABC có góc A S B ^ = B S C ⏜ = C S A ⏜ = 60 0 và SA=2, SB=3, SC=4. Tính thể tích khối S.ABC. ...
Đọc tiếp

Cho khối S.ABC có góc A S B ^ = B S C ⏜ = C S A ⏜ = 60 0 và SA=2, SB=3, SC=4. Tính thể tích khối S.ABC.
#Toán lớp 12
1
CM
Cao Minh Tâm
6 tháng 1 2019

Đúng(0)
PT
Pham Trong Bach
5 tháng 4 2017
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a .  Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.   A. a 3 2 B.  a 3 6 C.  a 3 24 D.  a 3 12 ...
Đọc tiếp

Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a .  Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.

 


A. a 3 2

B.  a 3 6

C.  a 3 24

D.  a 3 12

#Mẫu giáo
1
CM
Cao Minh Tâm
5 tháng 4 2017

Đúng(0)
PT
Pham Trong Bach
30 tháng 3 2018

Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.

A.  V = 1 6 a b c

B. V = 1 3 a b c

C. V = a b c

D. V = 1 2 a b c

#Toán lớp 12
1
CM
Cao Minh Tâm
30 tháng 3 2018

Đáp án A

Phương pháp:

 

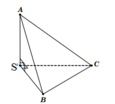
Thể tích khối chóp vuông

Cách giải:

S.ABC có SA, SB, SC đôi một vuông góc với nhau

⇒ S.ABC là tứ diện vuông tại đỉnh S

Đúng(0)
PT
Pham Trong Bach
6 tháng 1 2018
Cho khối chóp S . A B C có S A ,   S B ,   S C đôi một vuông góc với nhau và  S A = a ,   S B = b ,   S C = c . Tính thể tích khối chóp  S . A B C . ...
Đọc tiếp

Cho khối chóp S . A B C có S A ,   S B ,   S C đôi một vuông góc với nhau và  S A = a ,   S B = b ,   S C = c . Tính thể tích khối chóp  S . A B C .
#Toán lớp 12
1
CM
Cao Minh Tâm
6 tháng 1 2018

Đáp án A

Đúng(0)
PT
Pham Trong Bach
26 tháng 10 2018

Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC .

A.  V = 1 6 a b c

B. V = 1 3 a b c

C. V = abc

D.  V = 1 2 a b c

#Mẫu giáo
1
CM
Cao Minh Tâm
26 tháng 10 2018

Đáp án A

Đúng(0)
PT
Pham Trong Bach
8 tháng 12 2017

Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và S A = S B = S C = a .  Tính thể tích của khối chóp S. ABC.

A.  1 3 a 3

B.  1 2 a 3

C.  1 6 a 3

D.  2 3 a 3

#Mẫu giáo
1
CM
Cao Minh Tâm
8 tháng 12 2017

Đáp án là C

Đúng(0)
PT
Pham Trong Bach
15 tháng 5 2018
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thể tích của khối chóp S. ABC. ...
Đọc tiếp

Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thể tích của khối chóp S. ABC.
#Toán lớp 12
1
CM
Cao Minh Tâm
15 tháng 5 2018

Đáp án C

Đúng(0)
PT
Pham Trong Bach
15 tháng 3 2017
Cho khối S.ABC có góc A S B ^ = B S C ^ = C S A ^ = 60 ° và S A = 2 , S B = 3 , S C = 4.  Tính thể tích khối S.ABC. A. 2 2 B. 2 3 C. 4 3 D.  3 2 ...
Đọc tiếp

Cho khối S.ABC có góc A S B ^ = B S C ^ = C S A ^ = 60 ° và S A = 2 , S B = 3 , S C = 4.  Tính thể tích khối S.ABC.

A. 2 2

B. 2 3

C. 4 3

D.  3 2

#Mẫu giáo
1
CM
Cao Minh Tâm
15 tháng 3 2017

Đáp án A

Trên cạnh SB, SC lần lượt lấy M và N sao cho SA = SM = SN =2

Ta có SAMN là tứ diện đều cạnh 2, khi đó thể tích của tứ diện SAMN là  V S A M N = 2 2 3

Lại có  V S A M N V S A B C = S A S A . S M S B . S N S C = 1 3 ⇒ V S A B C = 3 V S A M N = 2 2

Đúng(0)
PT
Pham Trong Bach
11 tháng 3 2018
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, S A = S B = S C = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là A.  a 3 3 B. a 3 C. a 3 24 D. a 3 12 ...
Đọc tiếp

Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, S A = S B = S C = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là

A.  a 3 3

B. a 3

C. a 3 24

D. a 3 12

#Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 3 2018

Đáp án C

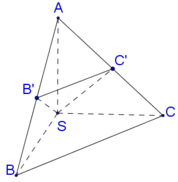
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.

Ta có: 

Đúng(0)
PT
Pham Trong Bach
14 tháng 2 2017
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là ...
Đọc tiếp

Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
#Toán lớp 11
1
CM
Cao Minh Tâm
14 tháng 2 2017

ĐÁP ÁN: A 

Đúng(0)
PT
Pham Trong Bach
22 tháng 8 2019
Cho hình chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥ SA ; SA = SB = SC = a .  Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là A. a 3 24 B.  a 3 C.  a 3 3 D.  a 3 12 ...
Đọc tiếp

Cho hình chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥ SA ; SA = SB = SC = a .  Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là

A. a 3 24

B.  a 3

C.  a 3 3

D.  a 3 12

#Mẫu giáo
1
CM
Cao Minh Tâm
22 tháng 8 2019

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP