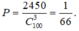Chọn ngẫn nhiên ba số tự nhiên trong các số từ 101 đến 200. Tính xác suất để ba số đó lập thành một cấp số cộng có công sai dương.
A . 3 100
B . 2 33
C . 1 66
D . 1 33
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Số cách chọn ra ngẫu nhiên 3 số từ A bằng C 100 3
Ta tìm số cách chọn ra bộ ba số thoả mãn:
Giả sử ba số chọn ra là
![]()
Ta có
![]()
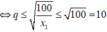
![]()
Mặt khác
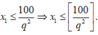
Với mỗi q ∈ 2 , 3 , . . . , 10 thì 100 q 2 cách chọn
và x 2 = q x 1 , x 3 = q 2 x 1 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
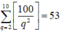
Xác suất cần tính bằng
53 C 100 3 = 53 161700

Chọn C
Lấy 3 phần tử từ tập S có ![]()
Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Đặt ![]() có 10 phần tử.
có 10 phần tử.
![]() có 10 phần tử.
có 10 phần tử.
a, b, c là ba số theo thứ tự lập thành cấp số cộng => 2a = b + c
Có 2a là số chẵn, nên b và c cùng chẵn hoặc cùng lẻ.
Suy ra số cách chọn b, c là ![]()
Mỗi cách chọn cặp b, c thì có duy nhất một cách chọn a sao cho 2a = b + c
Suy ra số phần tử của biến cố là ![]()
Xác suất thỏa yêu cầu bài là 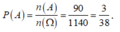
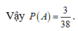

Số phần tử của không gian mẫu là: C 20 3 = 1140
Ba số a;b;c theo thứ tự lập thành CSC khi và chỉ khi a + c 2 = b ⇒ a + c = 2 b là số chẵn. Do đó a;c cùng chẵn hoặc cùng lẻ.
Như vậy, để ba số lấy được lập thành một cấp số cộng (giả sử 3 số đó là a , b , c a < b < c ) thì ta chọn trước 2 số a và c cùng chắn hoặc cùng lẻ.
Ta có
![]() .
.
Khi đó, luôn tồn tại duy nhất 1 số b thỏa mãn yêu cầu đề bài.
Số cách chọn bộ số a,c như trên là: 2 C 10 2 = 90
Xác suất cần tìm là: 90/1140=3/38,
Chọn C.
Chọn C
Ta có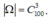
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng. Ta có các trường hợp sau:
Suy ra số kết quả lấy ra 3 số lập thành cấp số cộng là
Vậy số cách chọn thỏa mãn đề bài là